티스토리 뷰
[논문 리뷰]EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks
ProWiseman 2023. 2. 7. 18:50들어가며
본 글은 논문 EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks를 리뷰한 글입니다.
내용
기존의 한계
ConvNet을 스케일 업 할 때 보통 depth, width, image resolution을 스케일링하는 데, 이에 대한 제대로 된 이해가 없다.
- 스케일 업 할 때도 위 세 요소 중 하나만 스케일링한다.
- 2, 3가지도 임의로 스케일 할 수 있으나 수동으로 튜닝해야 하며 정확도와 효율성 또한 최적이 아니다.
AlexNet이후로 지속해서 모델의 크기가 커졌으나 하드웨어 메모리의 한계로 더 높은 정확도를 위해선 더 나은 효율성이 필요하다.
최근 MobileNet, SqueezNet, ShuffleNet이나 NAS(neural architecture search)로 네트워크의 width나 depth, 커널 타입 / 사이즈를 튜닝하며 정확도와 효율성을 트레이드하며 모델 압축을 하고 있으나 더 큰 모델로 확장하는 방법이 명확하지 않다.
앞선 연구에서도 깊이, 너비, 해상도를 균형있게 스케일링하는 시도가 있었으나 해당 연구는 수동으로 튜닝해 주었다.
논문의 키 아이디어
네트워크의 width/depth/resolution의 균형을 잘 잡는 것이 중요하다. (경험적으로 관찰)
- 균형만 잘 잡히면 각 요소를 일정한 비율로 확장하여 간단히 정확도와 효율성을 끌어올릴 수 있다.
- 이러한 관찰에 근거하여 혼합 스케일링 방법(compound scaling method)을 제안한다.
- 이 방법은 관행적인 방법과는 달리 네트워크의 width, depth, resolution을 균일하게 고정된 스케일링 계수에 따라 스케일링해주면 된다.

Compound Model Scaling
문제 정의
ConvNet의 \(i\)번째 레이어는 \(F_{i}\)를 오퍼레이터, \(Y_{i}\)를 출력 텐서, \(X_{i}\)를 \(<H_{i},W_{i},C_{i}>\)의 입력 텐서라 할 때\(Y_{i}=F_{i}(X_{i})\)로 정의될 수 있다. ConvNet을 \(N\)이라 할 때 \(N=F_{k}\bigodot...\bigodot F_{2}\bigodot F_{1}(X_{1})=\bigodot_{j=1...k}F_{j}(X_{1})\)와 같은 레이어를 엮은 리스트로 표현될 수 있다. 또한 ResNet과 같이 ConvNet의 각 스테이지의 레이어는 같은 아키텍처를 공유한다. 따라서 다음과 같이 표현할 수 있다.

여기서 \(F_{i}^{L_{i}}\)은 레이어 \(F_{i}\)가 \(i\) 번째 스테이지에서 \(L_{i}\)번 반복된다는 의미이다.
보통의 ConvNet이 \(F_{i}\)의 최선의 아키텍처를 찾는데 집중하는 반면 모델 스케일링은 이 \(F_{i}\)를 고정하고 레이어의 길이인 \(L_{i}\), 너비인 \(C_{i}\), 그리고/혹은 해상도인 \((H_{i},W_{i})\)를 확장해 보는 것이다. 이런 식으로 \(F_{i}\)를 고정하면 디자인 문제를 간소화할 수 있다. 그러나 여전히 각 레이어별로 \(L_{i}, C_{i}, H_{i}, W_{i}\)를 탐색하기엔 디자인 공간이 크므로 각 레이어 별로 균일하게 스케일링한다. 논문의 목표는 어떠한 리소스가 제한된 환경이 주어졌을 때 모델의 정확도를 최대화하는 것이다. 그리고 이는 최적화 문제로 정의될 수 있으며 다음과 같이 수식화 할 수 있다.

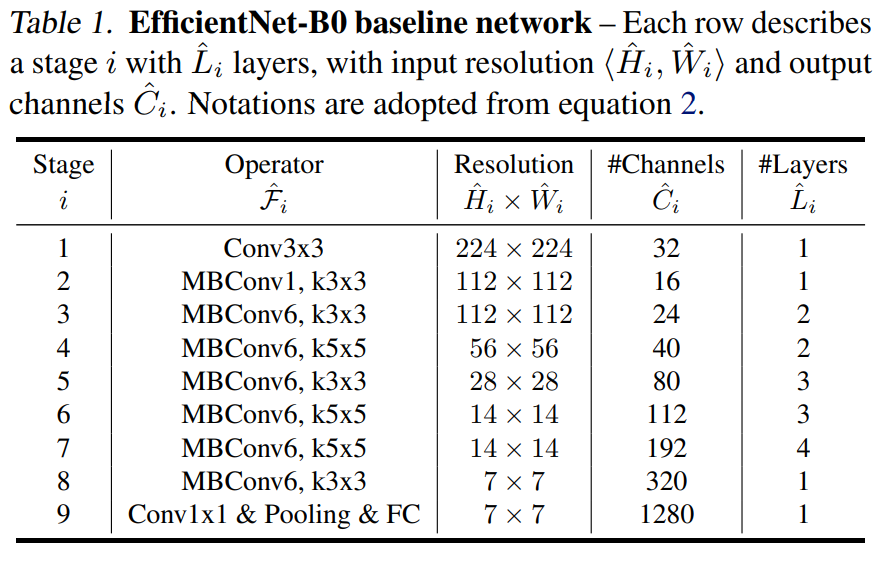
\(w, d, r\)은 각각 너비, 깊이, 해상도를 스케일링 하기 위한 계수이며 \(\widehat{F}_{i}, \widehat{L}_{i}, \widehat{H}_{i}, \widehat{W}_{i}, \widehat{C}_{i}\)은 베이스라인 네트워크에서 사전 정의되어 있는 파라미터이다.
Scaling Dimensions
앞서 정의한 문제의 주요 어려움은 \(d, w, r\)이 상호 의존적이고 리소스 제약에 따라 그 값이 변한다는 점이다. 이러한 문제 때문에 기존 모델들은 깊이, 너비, 해상도 중 하나만 스케일링하였다.
Depth(\(d\))를 조절하는 것은 가장 흔한 방법이며 직관적으로 깊은 ConvNet은 더 풍부하고 복잡한 피처를 포착할 수 있으며 새로운 태스크에서 더 잘 일반화 할 것 같다. 그러나 네트워크가 깊어질수록 vainishing gradient problem으로 인해 학습시키기 어려워진다. skip connection이나 batch normalization과 같은 테크닉들이 이런 현상을 완화해 주긴 하나 ResnNet-1000이 ResNet-101과 유사한 정확도를 보이는 것에서 볼 수 있듯 매우 깊은 네트워크에선 정확도 향상도 줄어든다. Figure 3에서 이러한 경향을 확인할 수 있다.
Width(\(w\))는 작은 사이즈의 모델에서 스케일링 할 때 자주 사용되며 넓은 네트워크가 fine-grained 피처를 더 잘 포착하는 경향이 있다고 한다. 그러나 극도로 넓고 얕은 네트워크는 고수준의 피처를 잘 포착하지 못하는 경향이 있다고 한다. Figure 3에서 볼 수 있듯 정확도 향상은 금방 포화(saturate)된다.
Resolution(\(r\))이 큰 입력 이미지일 수록 ConvNet은 잠재적으로 더 fine-grained 한 패턴을 포착할 수 있다. 초기 ConvNet은 224×224로 시작해서 현대의 ConvNet은 더 높은 정확도를 위해 299×299나 331×331을 사용한다. SOTA 모델도 480×480을 사용하며 객체 탐지 분야에서도 600×600이 널리 쓰인다. Figure 3에서 확인할 수 있듯 해상도가 높아지면 정확도가 개선되나 매우 높은 해상도에선 정확도 향상이 줄어든다.
위 내용을 종합하면 너비나 깊이, 해상도를 스케일링 하는 것 모두 정확도를 개선하나 모델이 커질수록 정확도 향상은 줄어든다.

Compound Scaling
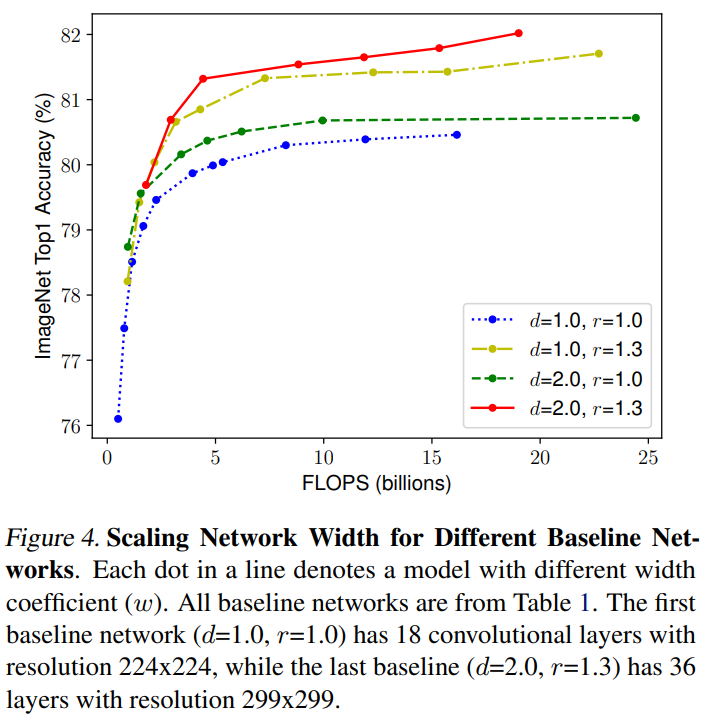
직관적으로 이미지 해상도가 커지면 네트워크의 깊이도 커져야 더 많아진 픽셀의 유사한 피처를 포착하는 데 도움이 된다. 너비도 마찬가지로 더 fine-grained 한 패턴을 포착하기 위해 이미지의 해상도가 커지면 너비도 함께 커져야 한다. 이러한 직관은 깊이와 너비, 해상도를 통합하고 균형을 맞춰야 한다고 말한다.
이 직관이 옳은지 검증하기 위해 Figure 4에 서로 다른 깊이와 해상도를 지닌 네트워크에 너비를 스케일링한 것을 비교했다. 깊이와 해상도를 변경하지 않은 네트워크의 경우 정확도가 금방 포화한다. 깊이와 해상도의 계수를 모두 2로 더 크게 만든 경우 같은 FLOPS에서 더 나은 정확도를 보였다.
위 내용을 종합하면 저 나은 정확도와 효율성을 추구하기 위해선 ConvNet 스케일링 과정에서 네트워크의 너비, 깊이, 해상도 모두의 균형을 맞추는 것이 중요하다는 것이다.
본 논문에선 혼합 계수인 φ 를 네트워크의 너비, 깊이, 해상도에 균일히 원칙적으로 사용하는 compound scaling method를 제안한다.
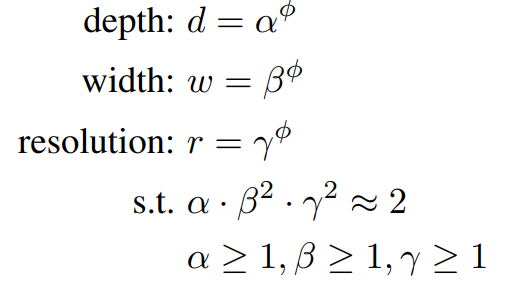
여기서 \(\alpha,\beta,\gamma\)는 작은 그리드 서치로 결정될 수 있는 상수이다. 그리고 φ 는 리소스를 얼마큼 더 쓸 수 있는지에 따라 유저가 정해주는 계수이다. 특히 FLOPS는 기존 합성공 연산자에선 \(d, w^{2}, r^{2}\)에 비례해서 늘어난다. 따라서 위 식의 경우 총 FLOPS는 \((\alpha\cdot\beta^{2}\cdot\gamma^{2})^{\phi}\)와 근사하게 증가할 것이다. 본 논문에선 \(\alpha\cdot\beta^{2}\cdot\gamma^{2}\approx 2\)로 제한한다.
EfficientNet Architecture
베이스라인 네트워크에서 레이어 오퍼레이터 별로 모델 스케일링을 바꾸지 않기 때문에 좋은 베이스라인 네트워크를 갖는 것 또한 중요하다. 평가는 기존 모델에서 할 예정이지만 더 좋은 시연을 위해 본 논문에선 EfficientNet이라 불리는 새로운 모바일 사이즈의 베이스라인을 개발했다.
정확도와 FLOPS 둘 다 최적화 하는 아키텍처를 찾았고 식은 \(ACC(m)×[FLOPS(m)/T]^{w}\) 이다. \(ACC(m)\)과 \(FLOPS(m)\)은 각각 모델 \(m\)의 정확도와 FLOPS를 의미한다. \(T\)는 목표하고자 하는 FLOPS이며 \(w\)는 정확도와 FLOPS 사이의 트레이트 오프를 조절하는 하이퍼파라미터로 -0.07로 정해주었다. 또한 어떤 하드웨어를 타겟으로 삼고 있지 않기에 레이턴시보단 FLOPS를 줄이는 방향으로 탐색하였다. 주요 블록은 mobile inverted bottleneck MBConv이다.
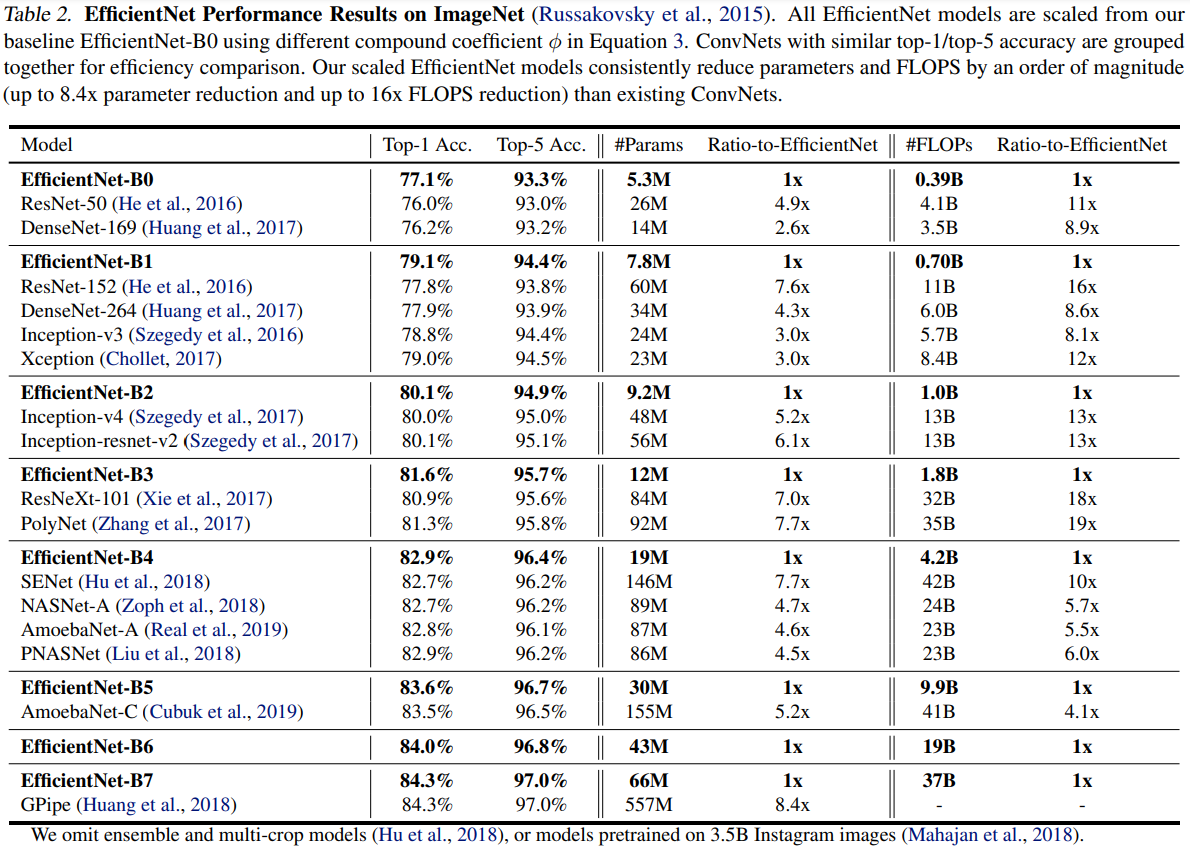
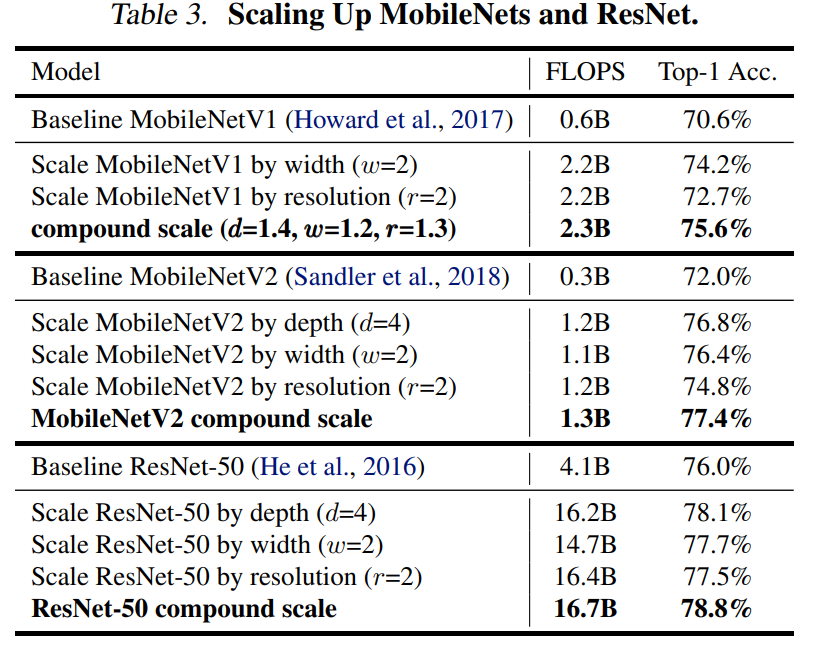
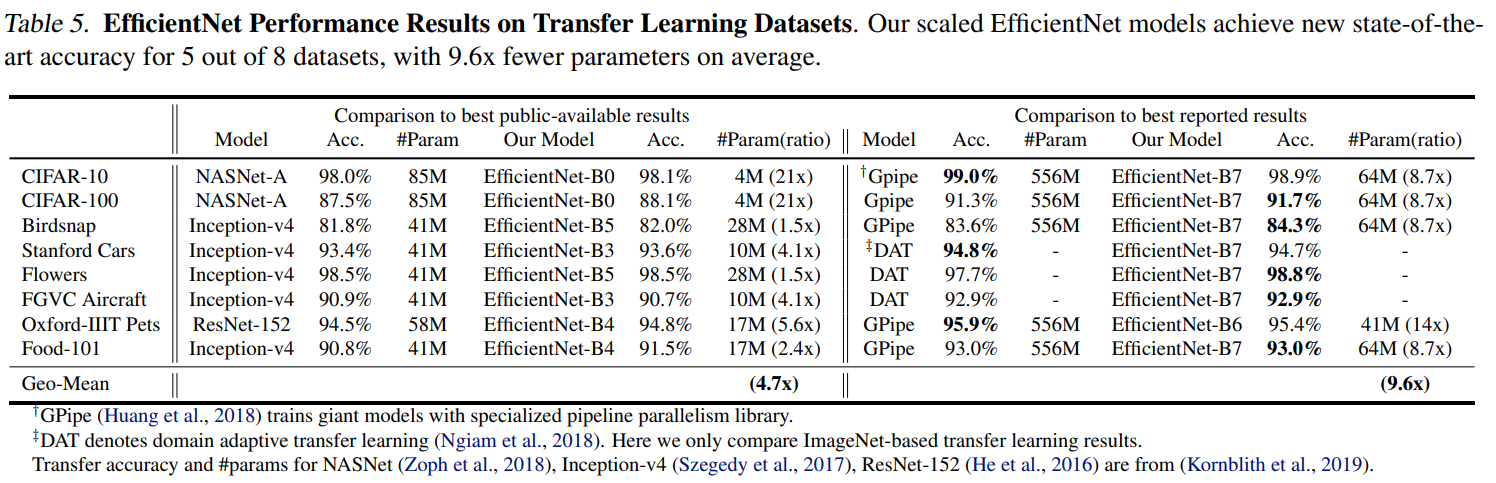
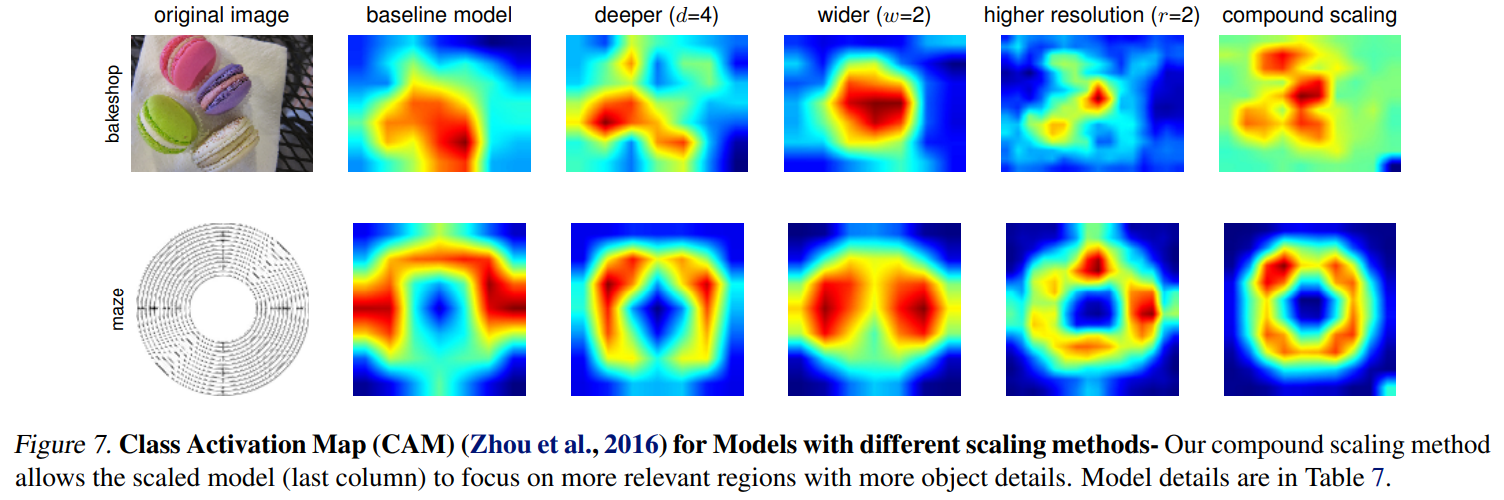
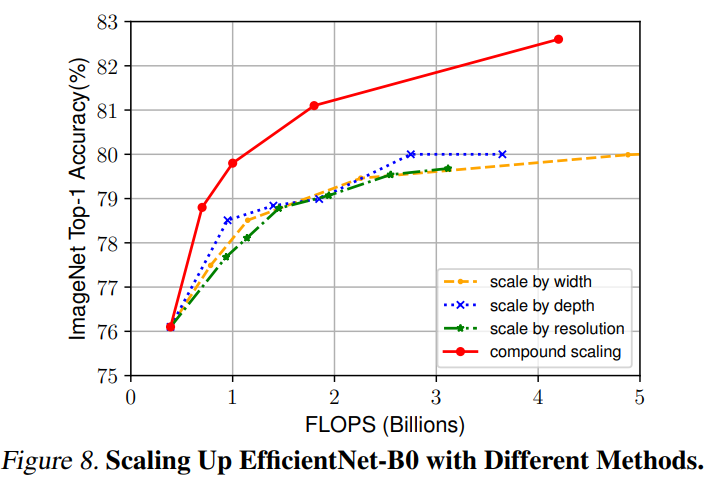
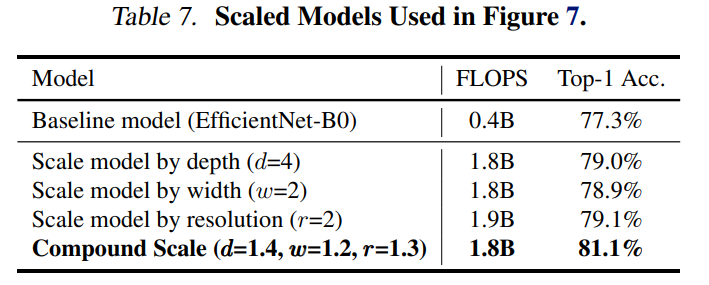
실험

'공부한 내용 정리 > 인공지능' 카테고리의 다른 글
| [논문 리뷰]Latent Aspect Rating Analysis on Review Text Data:A Rating Regression Approach (0) | 2023.02.27 |
|---|---|
| 인공지능 기초 1 (0) | 2023.02.24 |
| [논문 리뷰]You Only Look Once: Unified, Real-Time Object Detection (0) | 2023.01.22 |
| [논문 리뷰]EfficientNetV2: Smaller Models and Faster Training (0) | 2023.01.19 |
| [논문 리뷰]Sequence to Sequence Learning with Neural Networks (0) | 2023.01.19 |
