티스토리 뷰
공부한 내용 정리/인공지능
[논문 리뷰]Sequence to Sequence Learning with Neural Networks
ProWiseman 2023. 1. 19. 18:31들어가며
본 글은 Sequence to Sequence Learning with Neural Networks를 리뷰한 글입니다.
내용
논문의 키 아이디어
- LSTM으로 입력 시퀀스를 얽어 거대한 고정 차원 벡터 표현을 얻는다.
- 그 벡터로부터 출력 시퀀스를 뽑아내기 위해 또 다른 LSTM을 사용한다.
기존 DNN의 문제점
- 고정된 차원 벡터로 인코딩할 수 있는 문제에만 적용할 수 있다.
- 입력과 출력이 미리 정해지고 고정 돼야 한다.
- 여러 중요한 시퀀스 문제는 사전에 그 길이를 알 수 없다.
Model
Recurrent Neural Network
- 시퀀스에 대한 순전파 신경망의 자연스러운 일반화이다. (보통의 경우 이걸 쓴다는 느낌으로 이해했음)
- 입력을 \((x_{1},...,x_{T})\), 출력을 \((y_{1},...,y_{T})\)라 할 때 다음 식을 반복 연산한다.
\[ h_{t}=\mathrm{sigm}(W^{hx}x_{t}+W^{hh}h_{t-1}) \]
\[ y_{t}=W^{yh}h_{t} \]
- 입력과 출련간의 alignment가 미리 알려져 있을 때 sequence to sequence가 쉽다.
Recurrent Neural Network 단점
- 입력과 출력의 길이가 다르며 복합적이고 비단조적인 관계를 띨 경우 sequence to sequnce를 하기 어려워진다.
- 장거리 의존성(long term dependency) 문제가 있다.
LSTM
- 길이가 \(T\)인 입력 시퀀스를 \(x_{1},...,x_{T})\)이라 하고 이에 상응하는 길이가 \(T^{'}\)인 출력 시퀀스를 \(y_{1},...,y_{T^{'}}\)라 할 때 조건부 확률 \(p(y_{1},...,y_{T^{'}}|y_{1},...,y_{t-1})\)을 예측하는 모델이다.
- 장거리 시간 종속성 학습에 용이하다.
문제 극복 방법
- 입력 시퀀스를 하나의 RNN을 통해 고정된 크기의 벡터로 매핑하고 그 벡터를 또 다른 RNN이 목표 시퀀스로 매핑하는 것
- 장거리 시간 종속성 학습에 용이한 LSTM을 RNN 대신 사용하는 것
제안된 모델
- LSTM에 \((x_{1},...,x_{T})\)을 통과시켜 얻은 마지막 hidden state를 구한다. 이로부터 얻어진 것을 고정된 차원 표현 \(v\)라 하고 이로부터 조건부 확률을 계산한다.
- 그다음 최초 hidden state를 \(v\)로 하여 표준 LSTM-LM 공식으로 \(y_{1},...,y_{T^{'}}\)의 확률을 계산한다.
\[p(y_{1},...,y_{T^{'}}|x_{1},...,x_{T})=\prod_{t=1}^{T^{'}}p(y_{t}|v, y_{1},...,y_{t-1})\]
- 각 \(p(y_{t}|v, y_{1},...,y_{t-1})\)의 분포는 어휘 속 단어의 softmax로 표현된다.
- 모델이 가능한 모든 문장 길이에 걸쳐 분포를 정의할 수 있도록 "<EOS>" 심볼로 표현한다.
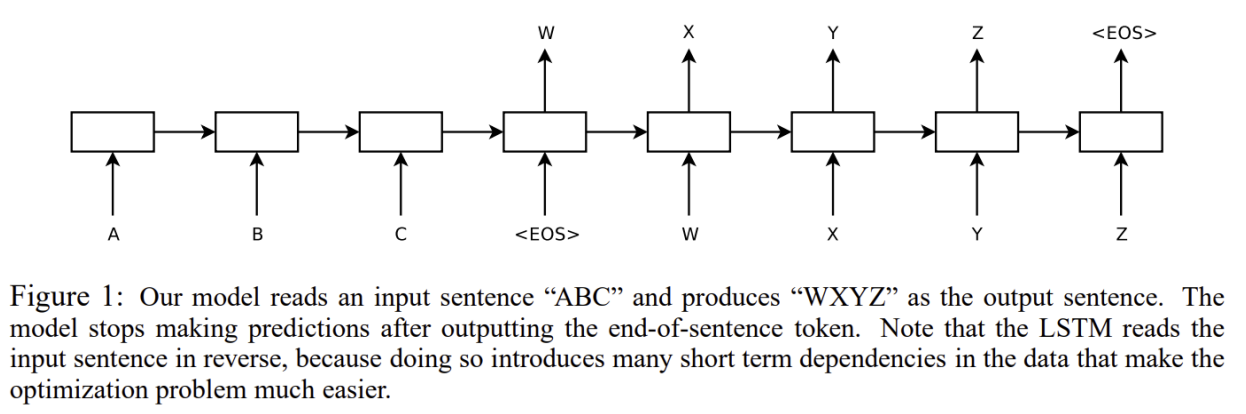
세부사항
- 두 개의 서로 다른 LSTM을 사용한다.
- 하나는 입력, 하나는 출력 시퀀스용
- 이렇게 할 경우 조금의 매개변수와 계산 비용 증가로 여러 언어쌍에서 동시에 자연스러운 LSTM을 학습할 수 있다.
- LSTM의 layer를 4로 설정한다.
- LSTM의 layer를 얕게 설정하는 것보다 깊게 설정하는 것이 훨씬 성능이 좋다.
- 입력 시퀀스의 단어 순서를 뒤집는다.
- 이렇게 하면 문장의 시작 부분이 서로 근접해지기 때문에 SGD가 신경망을 업데이트하기에 용이해진다.
- ex) a, b, c => 𝛼, 𝛽, 𝛾 대신 c, b, a = > 𝛼, 𝛽, 𝛾 로 LSTM을 통해 매핑
실험
WMT’14 English to French MT에 두 가지 방법을 적용했으며 Reference SMT 시스템 없이 바로 입력 시퀀스를 번역하도록 하였다.
Objective function
\(S\)가 입력 문장, \(T\)가 그에 따른 정답 번역이라 할 때 아래 식과 같이 log 확률을 최대화하는 방식으로 학습한다.
\[\frac{1}{|S|}\sum_{(T,S)\in S}\mathrm{log} p(T|S)\]
\[\widehat{T}=\mathrm{arg}\,\mathrm{\underset{T}{max}}\,p(T|S)\]
Decoding and Rescoring
- Beam search decoder로 가장 그럴듯한 번역을 탐색한다.
- 각 timestep 별로 가능한 가설을 늘려나가는데, 이런 식이면 가설이 너무 많아지므로 log 확률이 높은 것만 남겼다.
- 탐색된 1000개의 최선 리스트를 baseline으로 생성하고 LSTM으로 재채점 했다.
결과
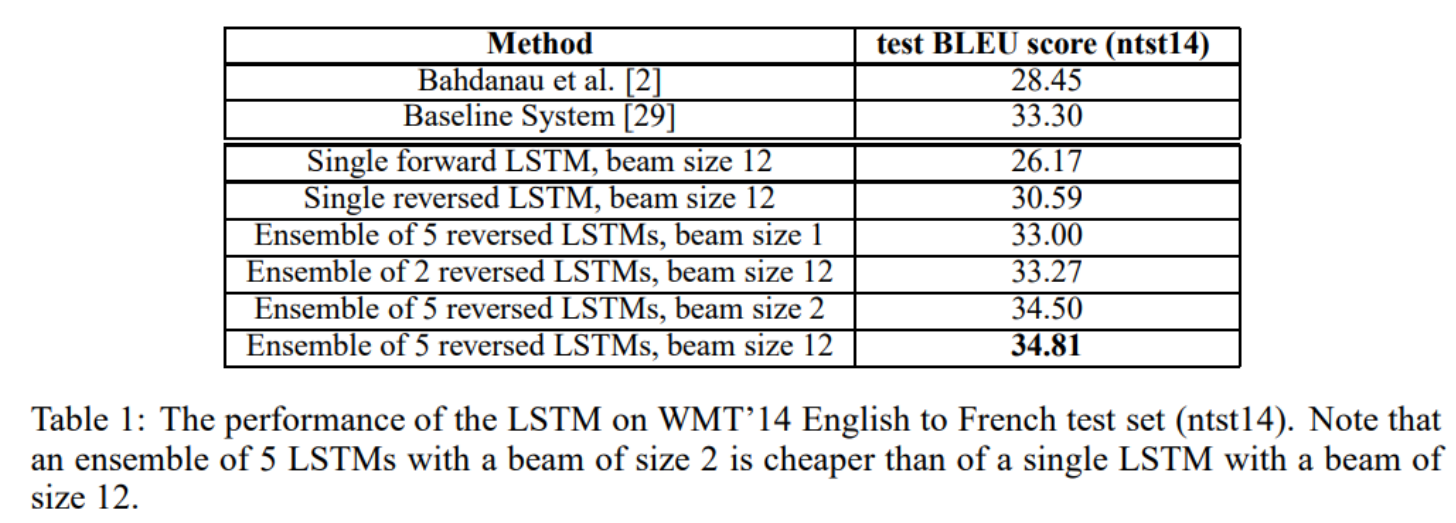

'공부한 내용 정리 > 인공지능' 카테고리의 다른 글
| [논문 리뷰]You Only Look Once: Unified, Real-Time Object Detection (0) | 2023.01.22 |
|---|---|
| [논문 리뷰]EfficientNetV2: Smaller Models and Faster Training (0) | 2023.01.19 |
| [논문 리뷰]Deep contextualized word representations (1) | 2023.01.16 |
| [TinyML]Tiny Machine Learning: The Next AI Revolution (0) | 2023.01.14 |
| StyleGAN / StyleGAN2 (2) | 2020.08.08 |
댓글
