티스토리 뷰
들어가며
본 게시물은 오일석 교수님의 기계학습 강의 1~2장을 보고 정리한 글입니다.
인공지능의 패러다임
기존 지식기반 방식은 광원, 그림자 등과 같은 변화에 취약했다. 따라서 데이터 중심의 접근방식인 기계학습으로 전환되었다.
기계학습
기계학습의 예측엔 예측값이 실수인 회귀(regression), 부류값인 분류(classification)가 있다.
기계학습은 가장 정확하게 예측할 수 있는 최적의 매개변수를 찾는 작업이다.
처음에는 실생활에서의 데이터의 피쳐는 매우 많기 때문에 복잡하여 최적값을 모르기에 점점 성능을 개선하여 최적에 도달한다.
기계학습의 궁극적인 목표는 훈련집합에 없는 새로운 샘플(테스트 집합)에 대한 오류를 최소화하는 것이며 이에 대한 높은 성능을 일반화(generalization) 능력이라 한다.
기계학습은 작은 개선을 반복하여 최적해를 찾아가는 수치적 방법이다. 기계 학습이 할 일을 공식화하면 다음과 같다.
\[\widehat{\Theta}=\underset{\Theta}{argmin}J(\Theta)\]
특징 공간
\(d\)-차원 데이터의 특징 벡터 표기 : \(x=(x_{1},x_{2},...x_{d})^{T}\)
\(d\)-차원 데이터를 모델에 학습시킬 경우
직선 모델
매개변수의 수 = \(d+1\)
\[y=w_{1}x_{1}+w_{2}x_{2}+\cdots w_{d}x_{d}+b\]
2차 곡선 모델
매개변수의 수 = \(d^{2}+d+1\), 학습해야 할 매개변수의 수가 기하급수적으로 늘어난다.
\[y=w_{1}x_{1}^{2}+w_{2}x_{2}^{2}+\cdots w_{d}x_{d}^{2}+w_{d+1}x_{1}x_{2}+\cdots +w_{d^{2}}x_{d-1}x_{d}+w_{d^{2}+1}x_{1}+\cdots +w_{d^{2}+d}x_{d}+b\]
특징 공간 변환과 표현 학습
아래 그림의 왼쪽과 같은 특징 공간에서 직선 모델을 적용하면 75% 정확률이 한계이다. 따라서 오른쪽 그림처럼 새로운 특징 공간으로 변환한다. 이러한 변환을 학습에 의해서 알아내는 것을 표현 학습 혹은 특징 학습이라 부른다.
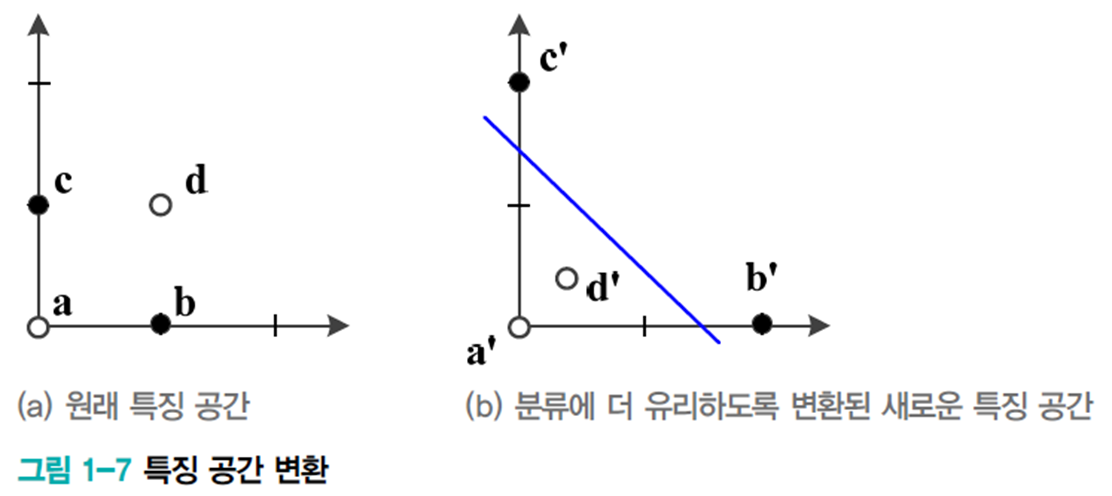
표현 학습(representation learning)
표현학습은 좋은 특징 공간을 자동으로 찾는 작업이다.
딥러닝은 다수의 은닉층을 가진 신경망을 이용하여 계층적인 특징 공간을 찾아낸다.
- 왼쪽 은닉층은 저급 특팅(에지, 구석점 등), 오른쪽은 고급 특징(얼굴, 바퀴 등)을 추출한다
특징공간은 차원에 무관하게 수식 적용이 가능하다. 예) 유클리디언 거리
\[\textit{dist}(a,b)=\sqrt{\sum_{i=1}^{d}(a_{i}-b_{i})^{2}}\]
보통 2~3차원의 저차원의 식을 고안한 다음 고차원으로 확장 적용한다.
차원의 저주
차원이 높아짐에 따라 계산 시간이나 메모리 공간과 같은 것이 기하급수적으로 늘어나 현실적으로 다룰 수 없는 상황을 의미한다. 따라서 기계학습은 이러한 차원의 저주를 피하기 위한 솔루션을 설계하는 것이 중요하다.
데이터에 대한 이해
과학기술은 데이터 수집, 모델 정립, 예측을 반복하는 방식으로 발전해 왔다. 기계학습도 마찬가지의 방법을 사용하는데, 기계학습이 해결하는 문제는 복잡하여 단순한 수학 공식으로 표현이 불가능하다. 따라서 자동으로 모델을 찾아내는 과정이 필수이다.
실제 기계학습의 경우 데이터 생성 과정을 알 수 없으므로 단지 주어진 훈련집합 \(\mathbb{X, Y}\)로 예측 모델 또는 생성 모델을 근사 추정 할 수 있을 뿐이다.
기계학습 모델이 높은 성능을 보이기 위해선 주어진 응용에 맞는 충분히 다양한 데이터를 충분한 양만큼 수집하여야 한다. ex) 정면 얼굴만 가진 데이터베이스로 학습하면 기운 얼굴은 매우 낮은 성능을 보인다. 따라서 주어진 응용 환경을 자세히 살핀 다음 그에 맞는 데이터베이스 확보는 아주 중요하다.
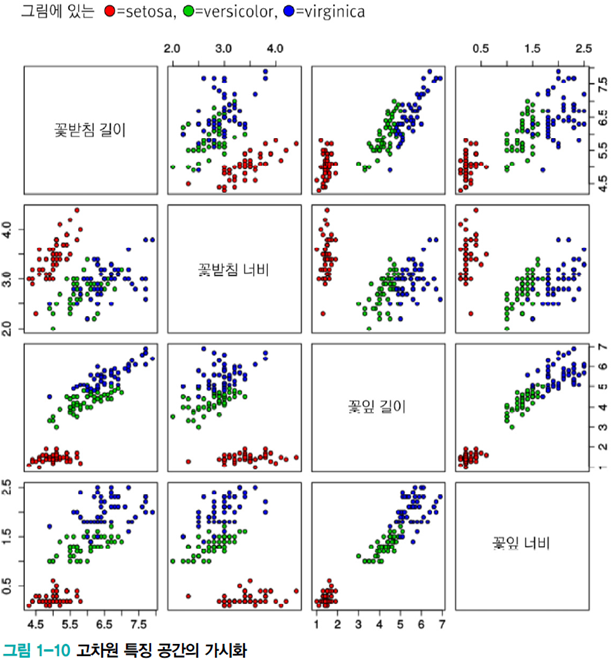
데이터베이스는 실제 특징 공간의 크기에 비해 매우 왜소하다. MNIST의 경우 만약 28*28의 흑백 비트맵이라면 서로 다른 총 샘플의 수는 \(2^{784}\)가지이지만 MNIST는 6만 개의 샘플만 가지고 있다. 그럼에도 기계학습은 높은 성능을 발휘하는데, 그 이유는 방대한 공간에서 실제 데이터가 발생하는 곳은 매우 작은 부분 공간이기 때문이다. 아래 그림에서 왼쪽과 같은 샘플의 발생 확률은 거의 0이다. 반면 오른쪽과 같이 일정한 규칙에 따라 매끄럽게 변화한다는 것(매니폴드 가정)을 기계학습이 잘 이용하고 있기 때문이다.


데이터 가시화를 하면 성능의 이유와 같은 여러 통찰력을 얻어 기계학습 알고리즘을 설계할 수 있다. 그러나 4차원 이상의 초공간은 한꺼번에 가시화할 수 없다. 이 점을 해소하기 위해 여러 기법들이 있다.
모델 선택
실제 세계의 데이터는 주로 선형이 아니며 잡음이 섞여 있으므로 비선형 모델이 필요하다.
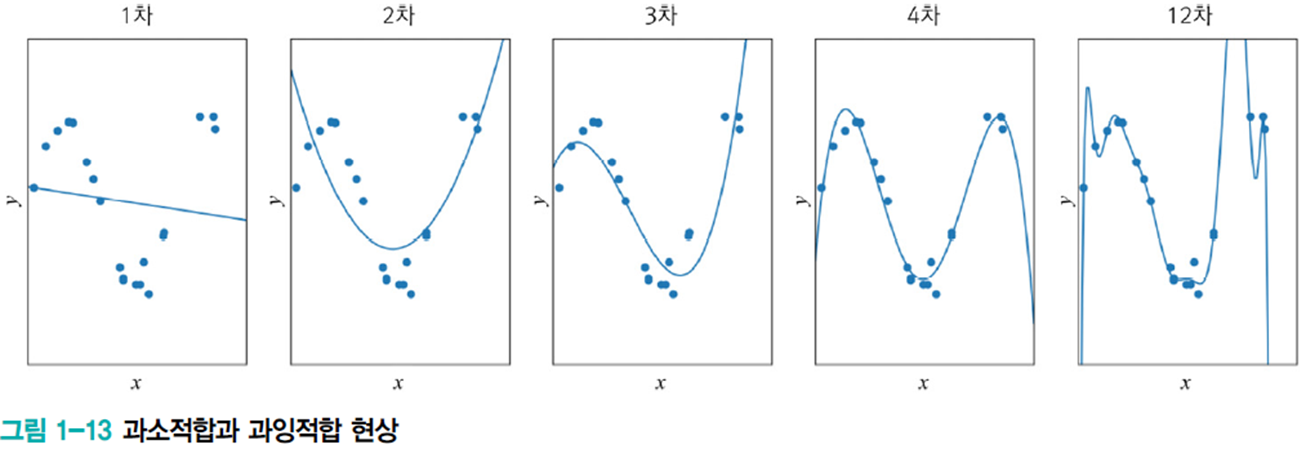
과소적합과 과잉적합
아래 그림에서 1차 모델은 과소적합이며 모델의 용량이 작아 오차가 클 수밖에 없는 현상을 의미한다.
2차, 3차, 4차, 12차는 비선형 모델을 사용하는 대안으로 다항식 곡선을 선택한 예이며 1차에 비해 오차가 크게 감소했다.
12차 모델의 경우 훈련 집합에 대해서 거의 완벽하게 근사화하였으나 새로운 데이터를 예측한다면 큰 문제가 발생한다. 모델의 용량이 크기 때문에 학습 과정에서 잡음까지 수용하여 과잉적합 현상이 발생한 것이다. 따라서 적절한 용량의 모델을 선택하는 모델 선택 작업이 필요하다.
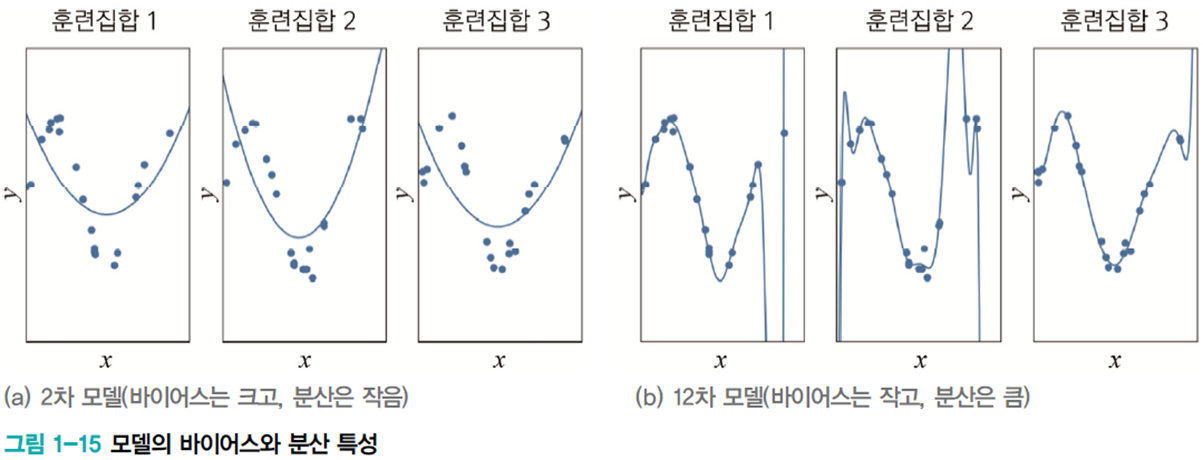
바이어스와 분산
훈련집합을 여러 번 수집하여 1~12차에 적용하는 실험
- 2차는 매번 큰 오차 -> 바이어스가 큼. 그러나 비슷한 모델을 얻음 -> 낮은 분산
- 12차는 매번 작은 오차 -> 바이어스가 작음. 그러나 크게 다른 모델을 얻음 -> 높은 분산
- 일반적으로 용량이 작은 모델은 바이어스는 크고 분산은 작다. 복잡한 모델은 바이어스는 작고 분산은 크다.
- 바이어스와 분산은 트레이드오프 관계이다.
기계학습의 목표는 낮은 바비어스와 낮은 분산을 가진 예측기를 제작하는 것이다. 즉 아래 그림에서의 왼쪽 아래의 상황이다.
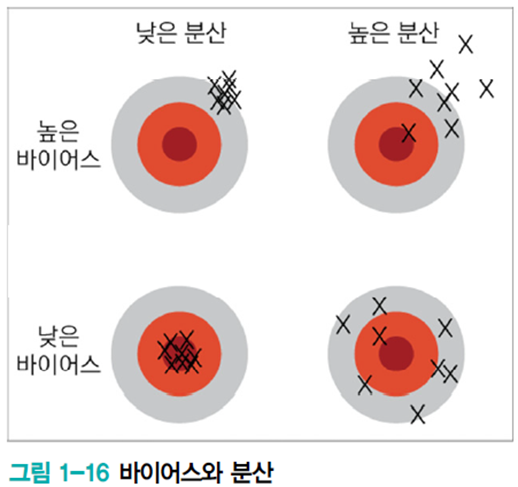
그러나 바이어스와 분산은 트레이드오프 관계이므로 바이어스 희생을 최소로 유지하며 분산을 최대로 낮추는 전략이 필요하다.
모델을 선택할 때는 검증집합과 교차 검증을 이용한다.
검증집합
데이터가 충분히 큰 경우 훈련집합, 테스트집합 외에 검증집합을 만들어 모델의 성능을 측정할 수 있다.

교차검증(cross validation)
비용 문제로 별도의 검증집합이 없는 상황에 유용한 모델 선택 기법이다. 훈련집합을 등분하여 학습과 평가 과정을 여러 번 반복한 후 평균을 사용한다.

부트스트랩(boot strap)
난수를 이용한 샘플링 반복이다. 매번 비슷한 비율로 샘플링한다.

현실에서는 식이 다항식 외에도 신경망, 강화학습, SVM, 트리 분류기 등 매우 다양한 모델이 있기 때문에 이미지 분류에선 CNN이 좋다와 같은 경험으로 큰 틀을 선택한 후 모델 선택 알고리즘의 세부 모델을 선택하는 전략을 취한다.
현대 기계 학습의 전략
용량이 충분히 큰 모델을 선택 후 선택한 모델이 정상을 벗어나지 않도록 여러 가지 규제(regularization) 기법을 적용한다.
규제
데이터 확대
데이터를 더 많이 수집하면 일반화 능력이 향상된다.
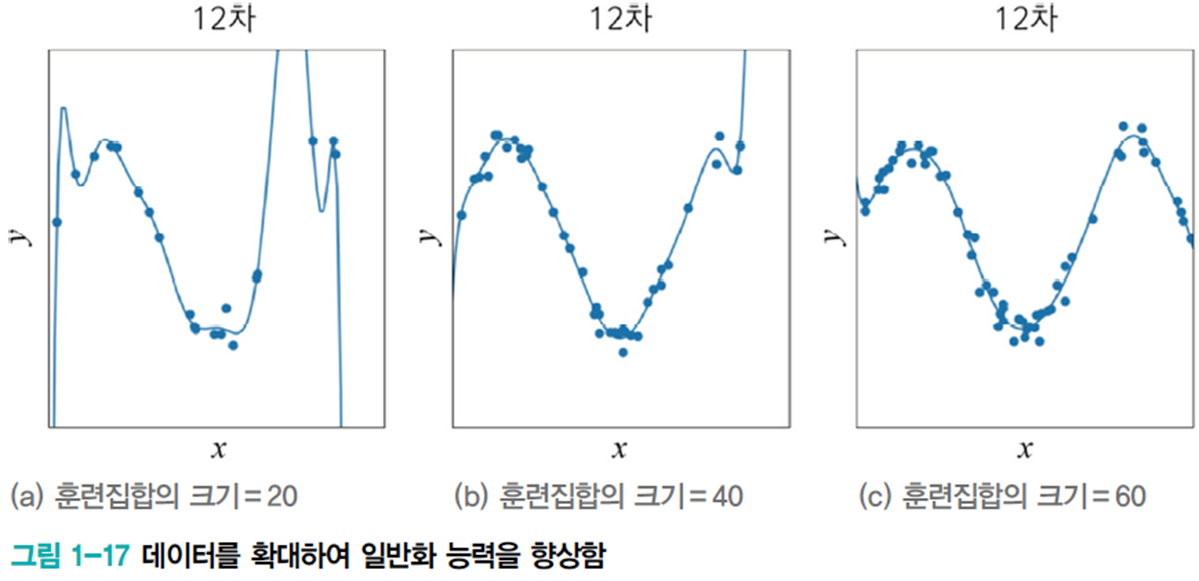
그러나 데이터 수집은 지도 학습의 경우 사람이 일일이 ground truth를 레이블링 하는 등 비용이 많이 든다. 따라서 인위적으로 데이터를 확대하는 방식을 사용한다.
훈련 집합에 있는 샘플을 회전, 스케일링, 와핑 등 변형한다.
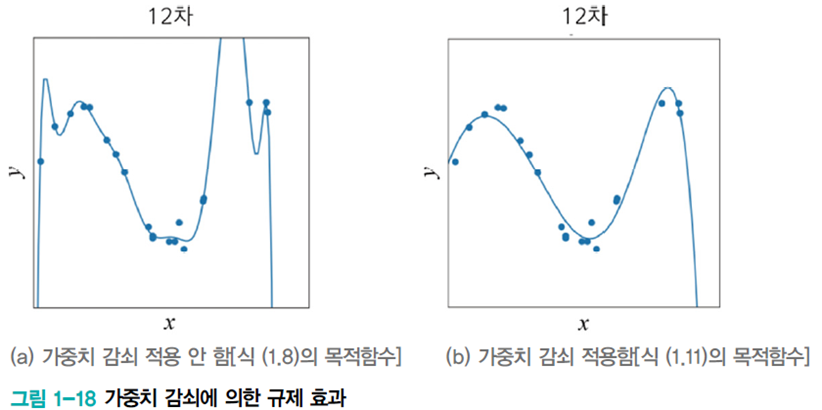
가중치 감쇠(weight decay)
아래 왼쪽 그림의 경우 가중치가 매우 크다.
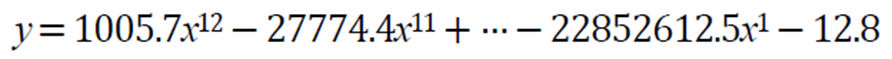
가중치 감쇠는 개선된 목적함수를 이용하여 가중치를 작게 조절하는 규제 기법이다. 다음과 같이 가중치가 크면 비용함수도 늘리는 규제 항을 추가하여 가중치 크기를 작게 유지한다.
\[J(\Theta)=\frac{1}{n}\sum_{i=1}^{n}(f_{\Theta}(x_{i})-y_{i})^{2}+\lambda \left\| \Theta\right\|_{2}^{2}\]
기계학습 유형
지도학습
특징 벡터 \(\mathbb{X}\)와 목푯값 \(\mathbb{Y}\)가 주어진 상황이다. 회귀와 분류 문제가 대표적이다.
비지도학습
특징 벡터 \(\mathbb{X}\)는 주어지지만 목푯값 \(\mathbb{Y}\)가 주어지지 않은 상황이다. 군집화 과업, 밀도 추정, 특징 공간 변환 과업이 대표적이다.
강화학습
목푯값이 주어지나 지도학습과는 다른 형태이다. 게임을 예로 들 경우 이기면 1, 패하면 -1의 목표값이 주어지는데 이를 게임을 구성한 샘플들 각각에 목푯값을 나누어 준다.
준지도 학습
일부는 \(\mathbb{X}\)와 \(\mathbb{Y}\)를 모두 가지지만, 나머지는 \(\mathbb{X}\)만 가진 상황이다.
인터넷 적분에 \(\mathbb{X}\)의 수집은 쉽지만 \(\mathbb{Y}\)는 수작업이 필요하여 최근 중요성이 부각된다.
기계학습과 수학
기계 학습에서 수학은 목적함수를 정의하고 목적함수가 최저가 되는 점을 찾아주는 최적화 이론을 제공한다.

선형대수
벡터
샘플을 특징 벡터(feature vector)로 표현한다.
iris 데이터에서 꽃받침의 길이/너비, 꽃잎의 길이/너비라는 4개의 특징이 각각 5.1, 3.5, 1.4, 0.2인 샘플의 경우 다음과 같이 표시한다.
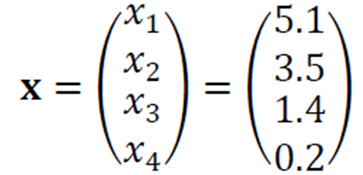
iris는 샘플이 150개가 있으므로 다음과 같이 여러 벡터로 표시할 수 있다.
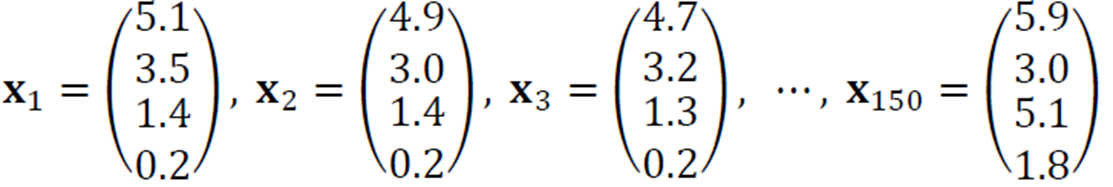
행렬
행렬은 여러 개의 벡터를 담는다. 훈련집합을 담은 데이터를 설계행렬이라 부르며 Iris 데이터를 설계행렬 \(X\)로 표현하면 다음과 같다.
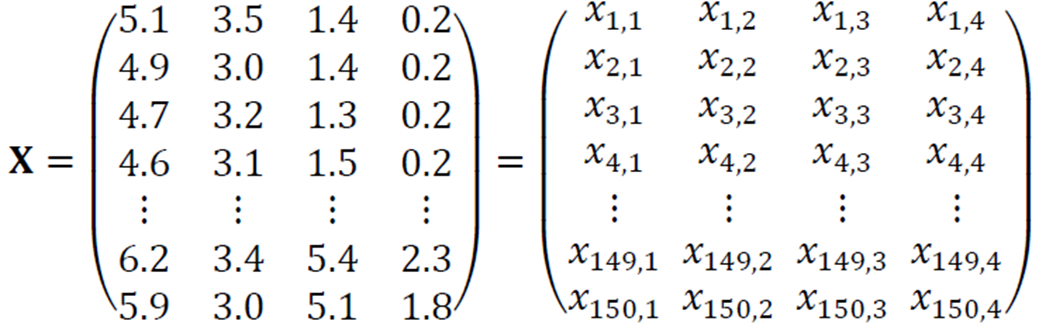
전치행렬
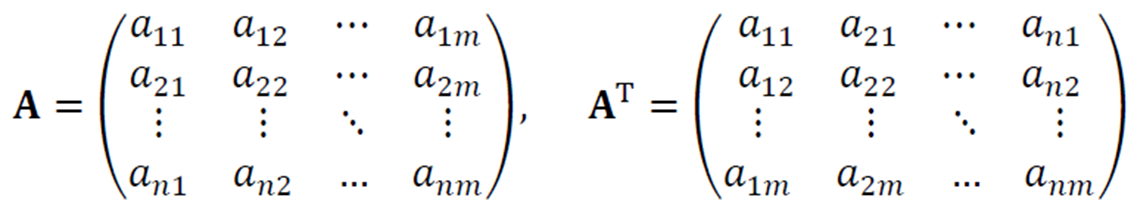
행렬을 이용하면 수학을 간결히 표현할 수 있다.
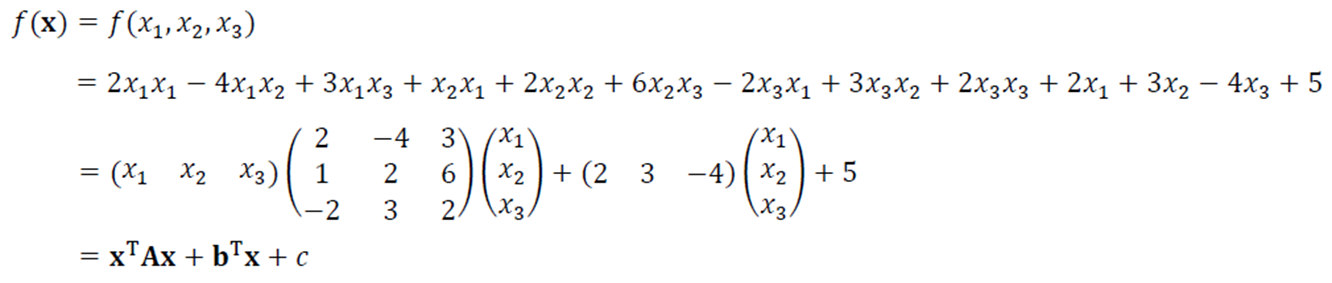
특수한 행렬

정사각행렬 : 행과 열의 개수가 같은 행렬
대각행렬 : 대각선 요소만 0이 아니고 외의 요소는 0인 행렬
단위행렬 : 대각 요소가 전부 1인 대각행렬
대칭행렬 : 대각선을 중심으로 대칭인 행렬
행렬 연산
행렬 곱셉 \(\mathbf{C=AB}\), 이때 \(c_{ij}=\sum_{k=1,s}a_{i,k}b_{k,j}\)
교환법칙은 성립하지 않는다. \(\mathbf{AB\neq BA}\)
분배법칙과 결합법칙은 성립한다. \(\mathbf{A(B+C)=AB+AC, A(BC)=(AB)C}\)
벡터의 내적 \(\mathbf{a \cdot b=a^{T}b}=\sum_{k=1,d}a_{k}b_{k}\)
텐서
3차원 이상의 구조를 가진 숫자 배열 ex) 3차원 구조의 RGB 컬러 영상
놈(norm)
벡터와 행렬의 크기를 놈으로 측정한다.
벡터의 \(p\)차 놈 : \(\left\| x\right\|_{p}=(\sum_{i=1,d}\left| x_{i}^{p}\right|)^{\frac{1}{p}}\)
최대 놈 : \(\left\| x\right\|_{\infty }=\textrm{max}(\left| x_{1}\right|,\left| x_{2}\right|,\cdots \left| x_{d}\right|)\)
프로베니우스 놈 : \(\left\| \mathbf{A}\right\|_{F}=\left ( \sum_{i=1,n}\sum_{j=1,m}a_{ij}^{2} \right )^{\frac{1}{2}}\)
유사도

코사인 유사도 : 정보의 검색에 자주 이용된다.
\[\boldsymbol{cosine_similarity}(a,b)=\frac{a}{\left\| a\right\|} \cdot \frac{b}{\left\| b\right\|}=cos(\theta)\]
퍼셉트론
딥러닝은 퍼셉트론을 여러 개 쌓은 형태
\(d\)차원의 특징 벡터와 \(d\)차원의 가중치, 즉 두 개의 \(d\)차원 벡터를 내적 하는 일을 한다.
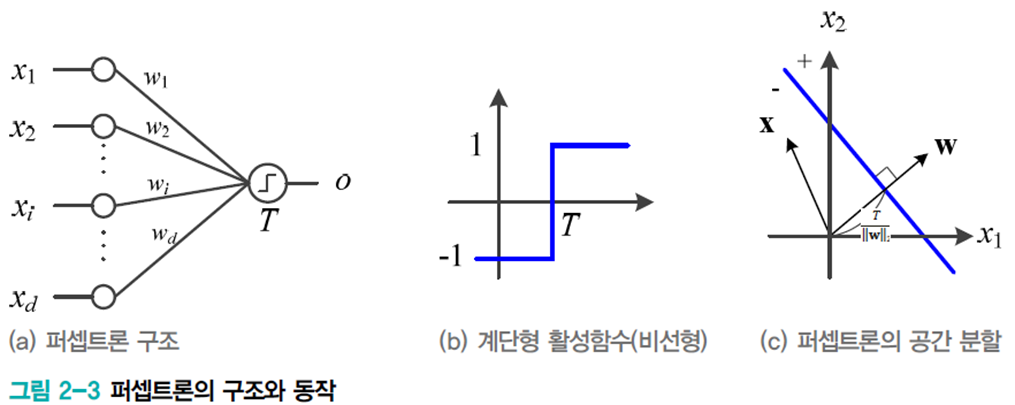
이를 수식으로 표현하면 \(o=\mathbf{\tau(w \cdot x)}\), 이때 \(\tau(a)=\left\{\begin{matrix}1 & a\geq T \\-1 & a< T \\\end{matrix}\right.\). \(\tau\)는 활성함수로 여기선 계단함수이다.
출력이 여러 개인 퍼셉트론
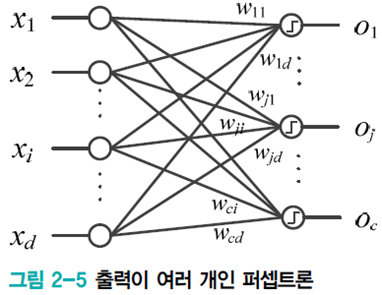
출력을 벡터 \(\mathbf{o}=(o_{1},o_{2},\cdots ,o_{c})^{T}\)로, \(j\)번째 퍼셉트론의 가중치 벡터를 \(\mathbf{w}_{j}=(w_{j1},w_{j2},\cdots ,w_{jd})^{T}\)와 같이 표기하고
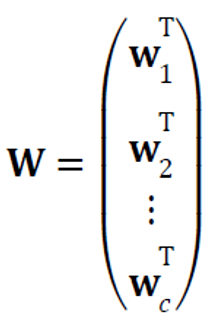
\(\mathbf{W}\)를 위와 같이 표기할 때 \(\mathbf{o=\tau(Wx)}\)로 간략하게 표기할 수 있다.
가중치 벡터를 각 부류의 기준 벡터로 간주하면 \(c\)개 부류의 유사도를 계산하는 셈이다.
퍼셉트론에서 \(\mathbf{W}\)를 모르기 때문에 학습은 훈련집합의 샘플에 대해 가장 잘 만족하는 \(\mathbf{W}\)를 찾아내는 것이라고 할 수 있다.
선형결합과 벡터공간
선형결합으로 만들어지는 공간을 벡터공간이라고 부른다.
역행렬
정사각행렬 \(\mathbf{A}\)의 역행렬 \(\mathbf{A}^{-1}\)이라 할 때
\[\mathbf{A}^{-1}\mathbf{A}=\mathbf{A}\mathbf{A}^{-1}=\mathbf{I}\]
이다.
역행렬은 다음과 같은 필요충분조건의 성질을 가진다.
- \(\mathbf{A}\)는 역행렬을 가진다. 즉, 특이행렬이 아닌다.
- \(\mathbf{A}\)는 최대계수를 가진다.
- \(\mathbf{A}\)의 모든 행이 선형독립이다.
- \(\mathbf{A}\)의 모든 열이 선형독립이다.
- \(\mathbf{A}\)의 행렬식은 0이 아니다.
- \(\mathbf{A^{T}A\)는 양의 정부호 대칭 행렬이다.
- \(\mathbf{A}\)의 고윳값은 모두 0이 아니다.
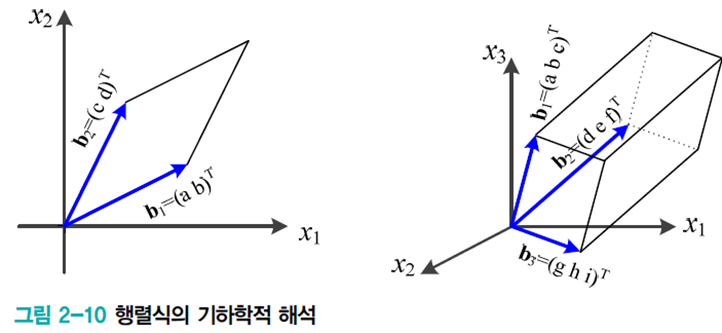
행렬식
행렬 \(\mathbf{A}\)의 행렬식 \(det(\mathbf{A})\)의 기하학적 의미는 다음과 같다.
- 2차원에서는 2개의 행 벡터가 이루는 평행사변형의 넓이
- 3차원에서는 3개의 행 벡터가 이루는 평행사각기둥의 부피
정부호 행렬
행렬의 부호를 나타낸다.
양의 정부호 행렬 : 0이 아닌 모든 벡터 \(\mathbf{x}\)에 대해 \(\mathbf{x^{T} Ax}>0\)
행렬 분해
정수 3717을 3*3*7*59로 소인수 분해할 수 있듯 행렬도 분해할 수 있다.
고윳값과 고유 벡터는 고유벡터 \(\mathbf{v}\)와 고윳값 \(\mathbf{\lambda}\)를 \(\mathbf{Av=\lambda v}\)로 표현될 수 있는 값을 말한다.
만약 행렬 \(\begin{pmatrix} 2& 1\\ 1& 2\\ \end{pmatrix}\)가 있을 때 \(\begin{pmatrix} 2& 1\\ 1& 2\\ \end{pmatrix}\begin{pmatrix} 1 \\ 1\end{pmatrix}=3\begin{pmatrix} 1 \\ 1\end{pmatrix}\)와 \(\begin{pmatrix} 2& 1\\ 1& 2\\ \end{pmatrix}\begin{pmatrix} 1 \\ -1\end{pmatrix}=1\begin{pmatrix} 1 \\ -1\end{pmatrix}\)로 나타낼 수 있으므로 고윳값은 3과 1, 고유벡터는 \(\begin{pmatrix} 1 \\ 1\end{pmatrix}\)과 \(\begin{pmatrix} 1 \\ -1\end{pmatrix}\)이다.
\(n \times n\)행렬에선 고윳값과 고유벡터가 최대 \(n\)개 있다.
행렬에 벡터를 곱할 때, 고유벡터만이 기존 행렬의 방향을 바꾸지 않는다.
고윳값 분해(eigen value decomposition)
\(\mathbf{A=Q\Lambda Q^{-1}}\)
\(\mathbf{Q}\)는 \(\mathbf{A}\)의 고유 벡터를 열에 배치한 행렬이고 \(\mathbf{\Lambda }\)는 고윳값을 대각선에 배치한 대각행렬이다.
고윳값 분해는 정사각행렬에만 적용이 가능하기 때문에 기계 학습에서는 정사각행렬이 아닌 경우의 분해도 필요하므로 고윳값 분해는 한계를 가진다.
이 경우 특잇값 분해(SVD : singular value decomposition)을 사용한다.
특잇값 분해(SVD : singular value decomposition)
\(\mathbf{A=U\Sigma V^{T}}\)로 나타낼 수 있다.
\(\mathbf{U}\)는 \(\mathbf{AA^{T}}\)의 고유벡터를 열에 배치한 \(n*n\) 행렬을 의미한다.
\(\mathbf{V}\)는 \(\mathbf{AA^{T}}\)의 고유벡터를 열에 배치한 \(m*m\) 행렬을 의미한다.
\(\mathbf{\Sigma }\)는 \(\mathbf{AA^{T}}\)의 고윳값의 제곱근을 대각선에 배치한 \(n*m\) 대각행렬을 의미한다.
확률과 통계
기계학습이 처리할 데이터는 불확실한 세상에서 발생하므로 불확실성을 다루는 확률과 통계를 잘 활용해야 한다.
확률 변수(random variable)
윷놀이의 경우 도, 개, 걸, 윷, 모 다섯 가지의 경우가 나올 수 있다. 이 다섯 가지 경우 중 한 값을 갖는 변수를 확률변수라 하며 확률변수를 \(x\)라 할 때 \(x\)의 정의역은 {도, 개, 걸, 윷, 모}이다.
확률분포
발생할 수 있는 모든 값에 대해서 확률을 지정하면 그게 확률분포이다.
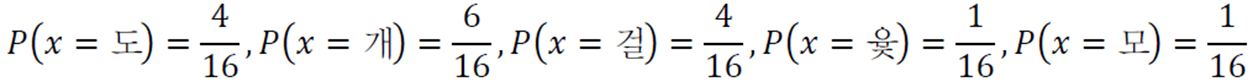

확률벡터(random vector)
확률변수처럼 하나의 스칼라가 아니고 Iris와 같이 여러개를 갖는 경우 확률벡터라고 한다.
\(\mathbf{x}=(x_{1},x_{2},x_{3},x_{4})^{T}\)
곱 규칙
\(P(y, x)=P(x|y)P(y)\)
합 규칙
\(P(x)=\sum_{y}P(y,x)=\sum_{y}P(x|y)P(y)\)
베이즈 정리
\(P(y, x)=P(x|y)P(y)=P(x, y)=P(y|x)P(x)\)이므로 다음과 같이 유도할 수 있다.
\[P(y|x)=\frac{P(x|y)P(y)}{P(x)}\]
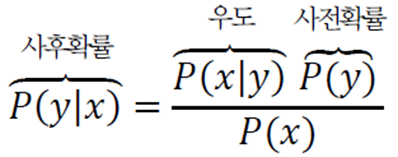
최대 우도
매개변수 \(\Theta \)를 모르는 상황에서 매개변수를 추정하는 문제이다.
최대 우도 추정 : \(\widehat{\Theta}=\underset{\Theta}{\textrm{argmax}P(\mathbb{X}|\Theta)}\)
이 경우 만약 샘플의 개수가 많아졌을 때 컴퓨터의 메모리는 한정되어 값이 점점 작아지다 0이 될 수도 있다. 이런 수치 문제를 피하기 위해 로그 표현을 사용한다.
최대 로그우도 추정 : \(\widehat{\Theta}=\underset{\Theta}{\textrm{argmax}}\textrm{ log}P(\mathbb{X}|\Theta)=\underset{\Theta}{\textrm{argmax}}\sum_{i=1}^{n}\textrm{ log}P(x_{i}|\Theta)\)
데이터의 요약 정보로서 평균과 분산
스칼라 값의 경우
평균 : \(\mu =\frac{1}{n}\sum_{i=1}^{n}x_{i}\)
분산 : \(\sigma^{2} =\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\mu)^{2}\)
벡터의 경우
평균 : \(\mathbf{\mu} =\frac{1}{n}\sum_{i=1}^{n}\mathbf{x}_{i}\)
분산(공분산 행렬) : \(\Sigma =\frac{1}{n}\sum_{i=1}^{n}(\mathbf{x_{i}-\mu})(\mathbf{x_{i}-\mu})^{T}\)
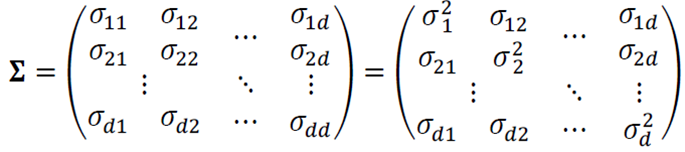
가우시안 분포
기본적인 1차원의 경우 다음과 같이 평균 \(\mu\)와 분산 \(\sigma^{2}\)로 정의된다.
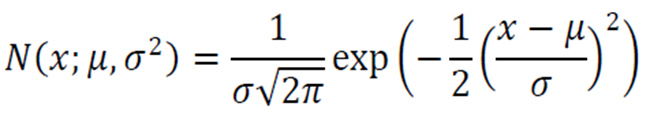
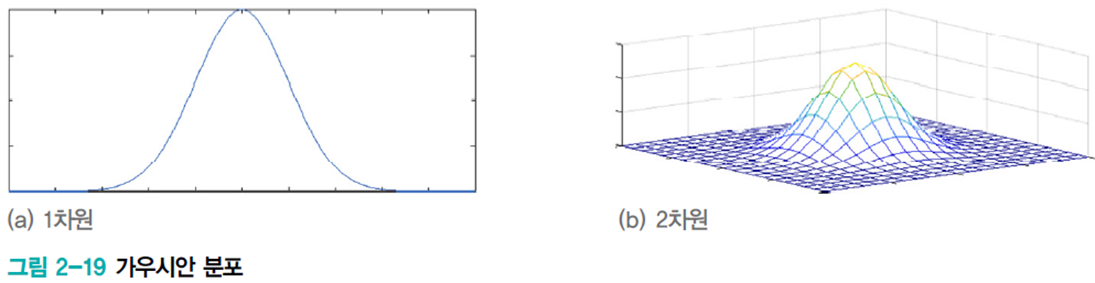
2차원 이상의 다차원 가우시안 분포에선 평균벡터 \(\mathbf{\mu}\)와 공분산행렬 \(\mathbf{\Sigma}\)로 정의된다.
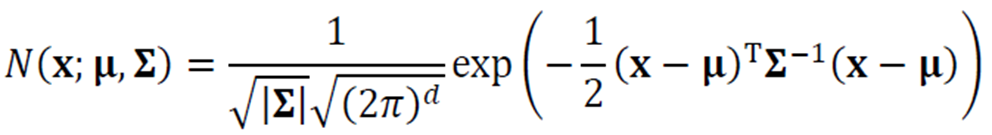
베르누이 분포
성공(\(x=1\)) 확률이 \(p\)이고 실패(\(x=0\)) 확률이 \(1-p\)인 분포
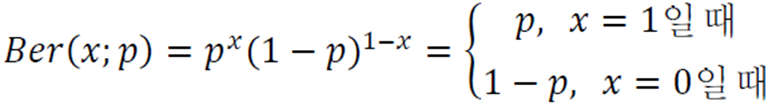
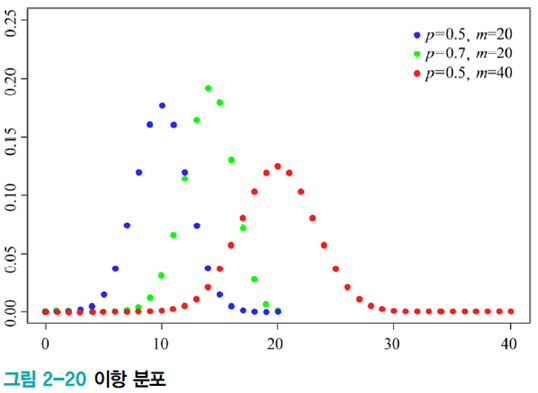
이항 분포
성공 확률이 \(p\)인 베르누이 실험을 \(m\)번 수행할 때 성공할 횟수의 확률분포
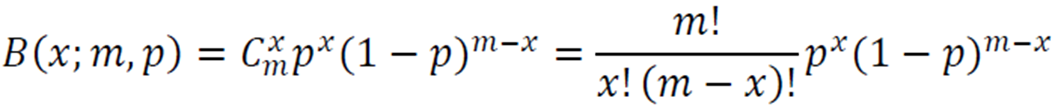
정보이론
메시지가 지닌 정보를 수량화가는 이론
이 정보의 기본 원리는 확률이 작을수록 많은 정보를 내포한다는 것이다.
자기 정보
사건(메시지) e_{i}의 정보량(단위: 비트(2의 경우) 또는 나츠(e의 경우))을 자기정보라 하는데, 이는 다음과 같이 계산한다.
\[h(e_{i})=-\mathrm{log}_{2}P(e_{i}) \textrm{ or } h(e_{i})=-\mathrm{log}_{e}P(e_{i})\]
엔트로피
확률 변수 \(x\)의 불확실성을 나타낸다. 불확실성이 높을수록 엔트로피가 높다.
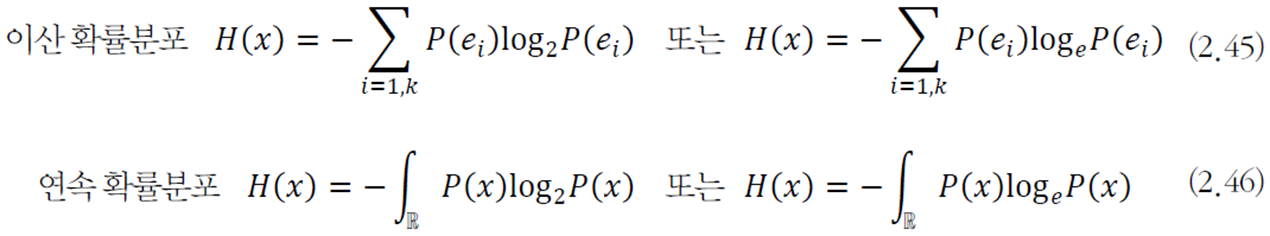
교차 엔트로피(cross entropy)
앞선 엔트로피의 경우 하나의 확률변수에 대한 불확실성이라면, 이 교차 엔트로피는 두 확률분포 사이의 불확실성을 나타낸다.
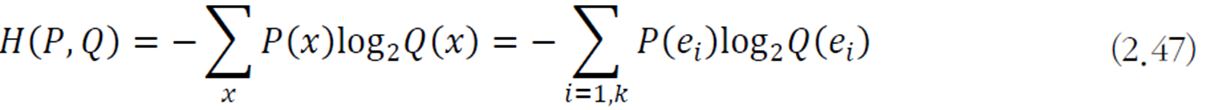
이를 전개하면 다음과 같다.
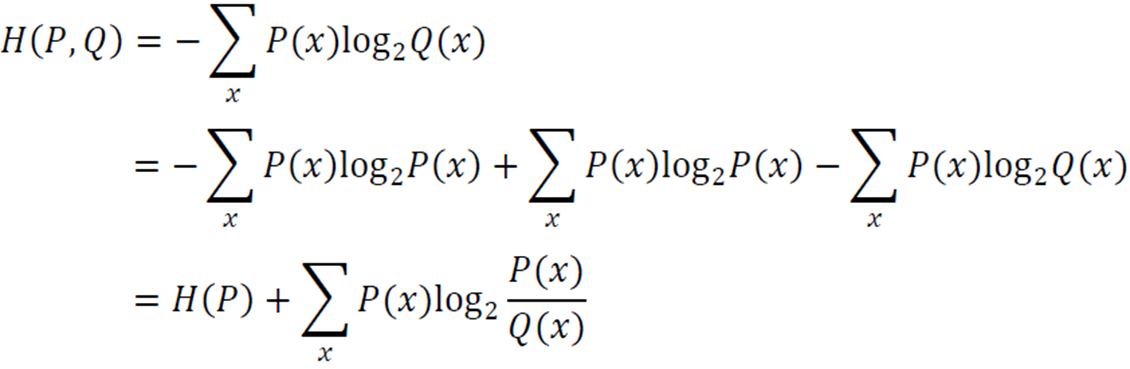
\(H(P)\)는 위에서 본 엔트로피 식과 같으므로 치환해주고 나머지 식을 계산해주어 뒤에 항이 만들어졌다. 이 항을 KL 다이버전스라고 한다.
KL 다이버전스
두 확률분포 사이의 거리를 계산할 때 주로 사용된다.
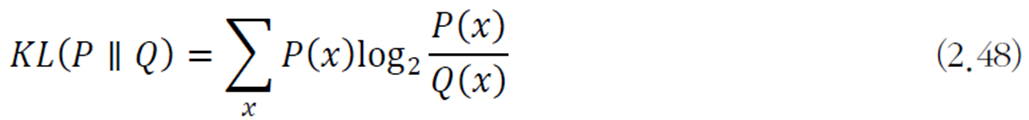
P와 Q의 인수 위치를 바꿔줬을 때 서로 값이 달라지기에 수학적으로 엄밀히 거리는 아니나 개념적으론 거리를 측정해주므로 기계학습에서 자주 쓰인다.
최적화 이론
순수 수학에선 식이 주어지고 해당 식의 최저점을 찾는 식으로 최적화를 하지만 기계학습에선 단지 훈련집합이 주어지고, 훈련집합에 따라 정해지는 목적함수의 최저점을 찾는다. 또한 훈련집합 뿐만 아니라 검증집합에서도 높은 성능을 보여야 한다. 이는 데이터로 미분하는 과정이 필요하며 주로 SGD를 사용한다.
높은 차원에 비해 훈련집합의 크기가 작아 참인 확률분포를 구하는 일이 불가능하다. 따라서 기계 학습은 적절한 모델을 선택하고, 목적함수를 정의하고, 모델의 매개변수 공간을 탐색하여 목적함수가 최저가 되는 최적점을 찾는 전략을 사용한다. (이는 특징 공간에서 해야하는 일을 모델의 매개변수 공간에서 하는 일로 대치한 셈이다.)

학습은 매개변수 공간 내에서 이루어지는데 이는 특징 공간보다 수 배-수만 배 넓다.
기계학습이 해야 할 일을 식으로 정리하자면 \(J(\Theta)\)를 최소로 하는 최적해 \(\widehat{\Theta}\)를 찾는 작업. 즉, \(\widehat{\Theta}=\underset{\Theta}{\textrm{argmin}}J(\Theta)\)로 정의 가능하다.
기계학습이 사용하는 전형적인 알고리즘
목적함수가 작아지는 방향을 주로 미분으로 찾아낸다.

미분에 의한 최적화
1차 도함수 \(f'(x)\)는 함수의 기울기, 즉 값이 커지는 방향을 지시한다. 따라서 \(-f'(x)\)방향에 목적함수의 최저점이 존재한다. 위 알고리즘에서 \(d\Theta\)로 \(-f'(x)\)를 사용한다. 이게 경사 하강 알고리즘의 핵심 원리이다.
편미분
변수가 여러 개인 함수의 미분이다.
각 매개변수에 대해서 미분값을 구한다음에 벡터형태로 표현하면 이를 그레이디언트라 부른다.
기계학습에선 매개변수가 매우 많으므로 편미분을 사용한다.
독립변수와 종속변수
최적화는 예측 단계가 아니라 학습 단계에 필요하므로 MSE를 예로 들면 \(\Theta\)가 독립변수이고 \(J(\Theta)\)가 종속변수이다.
\[J(\Theta)=\frac{1}{n}\sum_{i=1}^{n}(f_{\Theta}(x_{i})-y_{i})^{2}\]
연쇄법칙
합성함수를 미분하는 방법이다.
다층 퍼셉트론에서 역전파할 때 연쇄법칙을 적용한다.
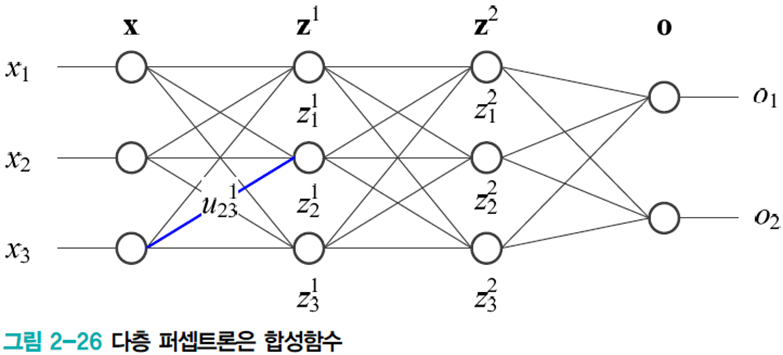
야코비언 행렬
차원을 변환해주는 행렬이다.
함수 \(\mathbf{f}:\mathbb{R}^{d}\mapsto \mathbb{R}^{m}\)
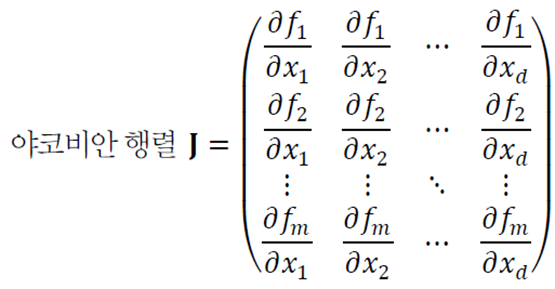
헤시안 행렬
야코비언의 2차 편도함수 버전이다.
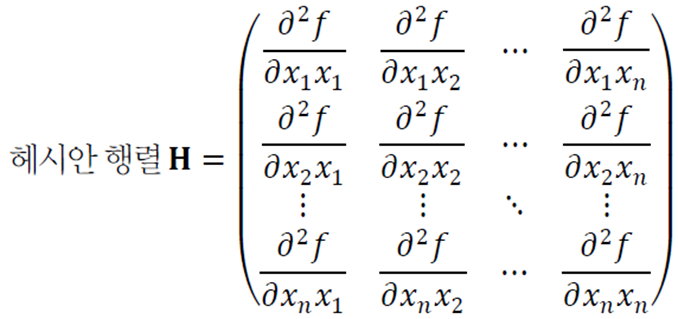
배치 경사 하강 알고리즘
샘플의 그레이디언트를 평균한 후 한꺼번에 갱신한다.

스토캐스틱 경사 하강 알고리즘
한 샘플의 그레이디언트를 계산한 후 즉시 갱신한다. epoch마다 샘플을 섞는다.

'공부한 내용 정리 > 인공지능' 카테고리의 다른 글
| 인공지능 기초 2 (0) | 2023.03.13 |
|---|---|
| [논문 리뷰]Latent Aspect Rating Analysis on Review Text Data:A Rating Regression Approach (0) | 2023.02.27 |
| [논문 리뷰]EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks (0) | 2023.02.07 |
| [논문 리뷰]You Only Look Once: Unified, Real-Time Object Detection (0) | 2023.01.22 |
| [논문 리뷰]EfficientNetV2: Smaller Models and Faster Training (0) | 2023.01.19 |
