티스토리 뷰
들어가며
본 게시물은 오일석 교수님의 기계학습 강의 4장을 보고 정리한 글입니다.
딥러닝
딥러닝이란 깊은 신경망을 학습시키는 알고리즘이다. (※ 깊은 신경망이란 다층 퍼셉트론에서 은닉층을 여러개 추가한 것이다.)
딥러닝은 현대 기계학습을 주도하며 음성인식, 글자인식, 얼굴인식 등 여러 인공지능 활용 분야에서 획기적인 성능 발전이 이루어졌다.
과거 딥러닝의 문제점
- 그레이디언트 소멸 문제 : 역전파 과정에서 출력층에서 입력층으로 갈 수록 미분값이 0에 가까워지는 그레이디언트 소멸 문제로 인해 신경망 층을 3개 이상 쌓은 것보다 1~2개 쌓은 것이 성능이 더 좋았다.
- 훈련 집합이 작았다.
- 컴퓨팅 자원의 성능이 떨어지고 가격도 비쌌다.
이러한 문제 해결을 위한 모색
- 학습률에 다른 성능 변화 양상
- 옵티마이저 모멘텀 영향
- 은닉 노드 수에 따른 성능 변화
- 데이터 전처리 ex) 데이터의 평균이 0이 되게 정규화, 분산 범위 조절
- 활성함수의 영향
- 규제 기법의 영향 etc..
딥러닝 성공의 요인
- 컨볼루션 신경망 (자세한 내용은 후술)
- 값싼 GPU
- 인터넷으로 인한 학습 데이터 증가
- 더 단순하며 효과적인 활성함수. 대표적으로 ReLU 등
- 과적합을 방지하기 위한 효과적인 다양한 규제 기법. 대표적으로 Data augmentation, Dropout, early stopping, ensemble 등
- 층별 예비학습 (지금은 잘 안쓰이나 초창기에 중요했음)
기계학습 패러다임
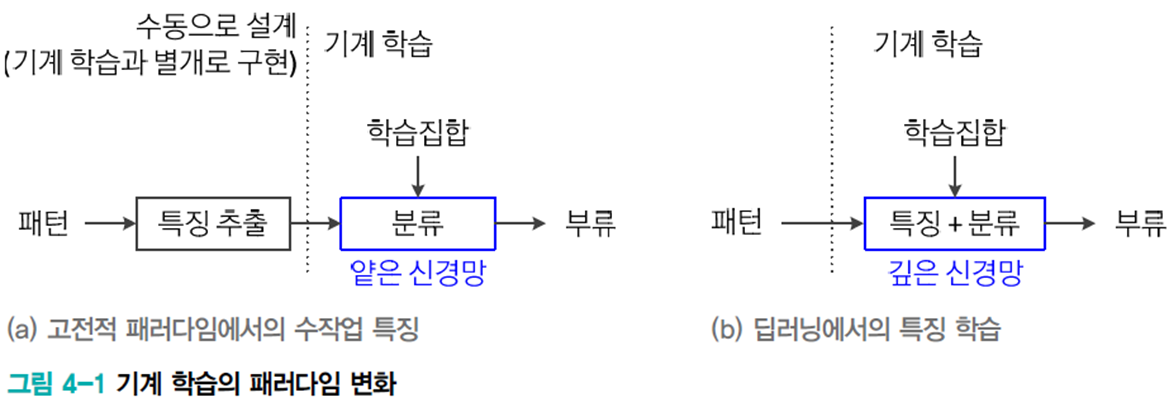
과거엔 사람이 직접 특징 추출기를 고안하여 이를 통해 추출된 특징을 분류기에 입력하는 식이었다.
딥러닝에선 특징 추출과 분류를 동시에 진행한다.
특징 추출을 학습으로 설계할 경우 특징 학습(feature learning)이라고 한다.
원래 패턴을 신경망의 입력으로 줄 경우 통째 학습(end-to-end learning)이라고 한다.
특징 학습(feature learning) 또는 표현 학습(representation learning)
특징 학습은 그림 4-2와 같이 보통 앞쪽을 특징 추출, 뒤쪽을 분류로 아키텍처를 구성한다.
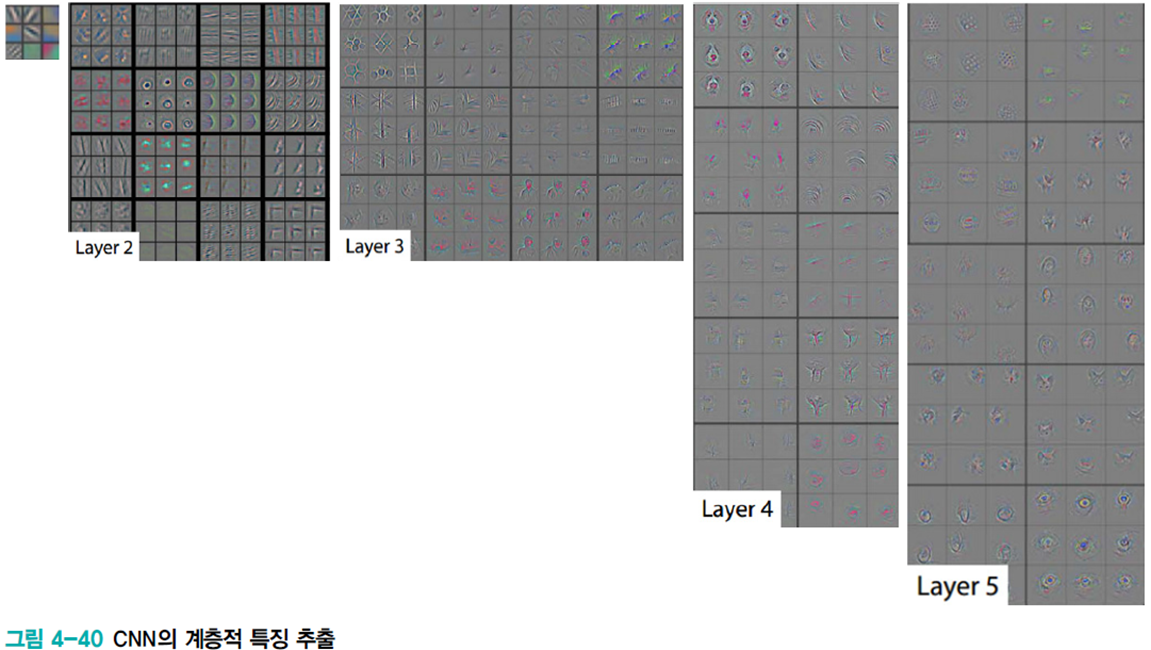
앞 단계의 은닉층일수록 에지나 코너와 같은 저급 특징을 추출하고, 뒷 단계로 갈수록 추상적인 고급 특징을 추출한다.

깊은 다층 퍼셉트론
DMLP(deep ML)의 구조
입력층(\(d+1\)개의 노드), 출력층(\(c\)개의 노드)
\(L-1\)개의 은닉층 (입력층은 0번째, 출력층은 \(L\)번째 은닉층으로 간주)
\(l\)번째 은닉층의 노드 수는 \(n_{l}\)

DMLP의 가중치 행렬은 다음과 같이 구성 돼 있다.
\(u_{ji}^{l}\)은 \(l-1\) 번째 층과 \(i\)번째 층의 \(j\) 번째 노드를 연결하는 가중치이다. 아래 보이는 가중치 행렬해서 각 행은 \(n_{l}\) 번째 은닉층의 가중치를 의미한다.
\(l-1\) 번째 층과 \(l\) 번째 층을 연결하는 가중치는 총 \(\left (n_{l-1} + 1\right )n_{i}\) 개가 된다.

DMLP의 동작은 다음과 같은 식으로 표시할 수 있다.
\(o=f(x)=f_{L}(\cdots f_{2}(f_{1}(x)))\)
이 동작을 구체화하면 다음과 같다.
\(z^{l}\)는 \(l\) 층의 입력 벡터이다.
입력층의 특징 벡터
\(z^{0}=(z_{0},z_{1},z_{2}, \cdots ,z_{n_{0}})^{T}=(1,x_{1},x_{2},\cdots ,x_{d})^{T}\)
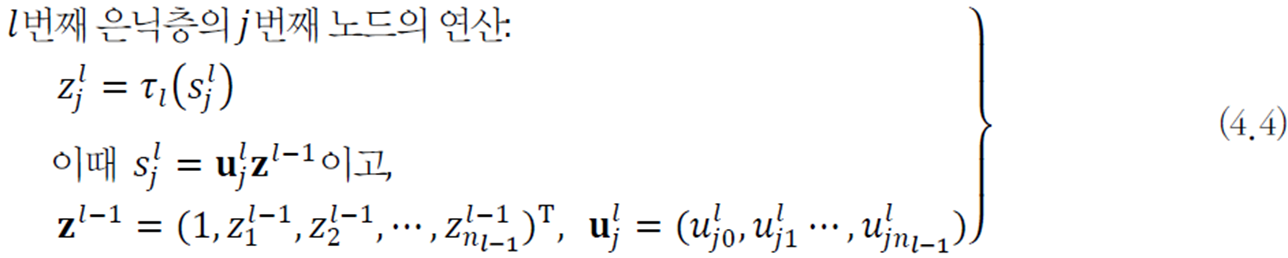
행렬 표기를 이용해 \(l\)번째 층의 연산 전체를 쓰면 다음과 같다.
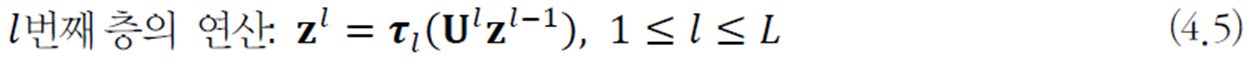
DMLP의 학습
MLP 학습과 유사하게 그레이디언트 계산과 가중치 갱신을 하지만 더 많은 단계에 걸쳐 수행한다.
오차 역전파 알고리즘
\(L\) 번째 층(출력층)의 그레이디언트 계산
\(\begin{matrix} \delta_{k}^{L}=\tau_{L}^{'}(s_{k}^{L})(y_{k}-o_{k}),& 1 \leq k \leq c \end{matrix}\)
\(\begin{matrix} \frac{\delta J}{\delta_{kr}^{L}}=-\delta_{k}^{L}z_{r}^{L-1},& 0 \leq r \leq n_{L-1}, 1 \leq k \leq c \\\end{matrix}\)
\(l+1\) 번째 층의 정보를 이용하여 \(l\) 번쨰 층의 그레이디언트 계산 (\(l=L-1,L-2,\cdots ,1\))
\(\begin{matrix} \delta_{j}^{l}=\tau_{l}^{'}(s_{j}^{l})\sum_{p=1}^{n_{l+1}}\delta_{p}^{l+1}u_{pj}^{l+1},& 1 \leq j \leq n_{I} \end{matrix}\)
\(\begin{matrix} \frac{\delta J}{\delta_{ji}^{l}}=-\delta_{j}^{l}z_{i}^{l-1},& 0 \leq i \leq n_{l-1}, 1 \leq j \leq n_{l} \\\end{matrix}\)

컨볼루션 신경망
DMLP와 CNN 비교 (영상에선 설명 X)
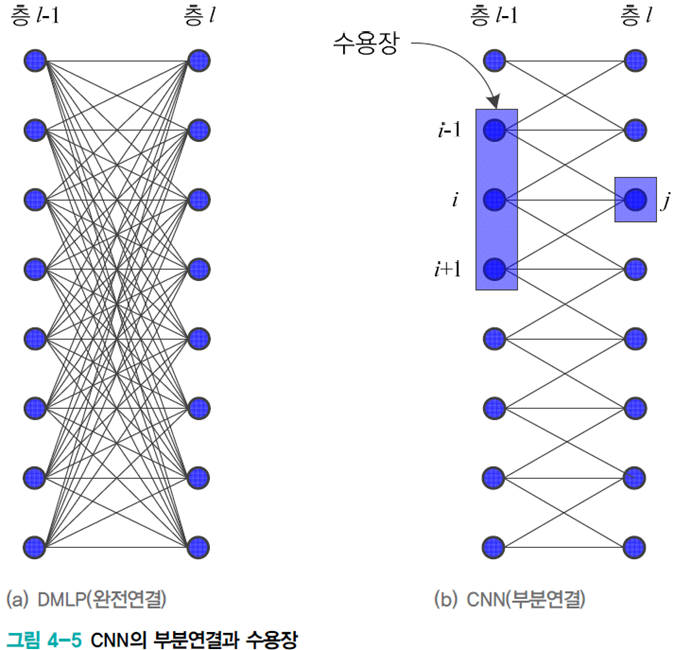
DMLP
- 완전연결 구조로 높은 복잡도
- 학습이 매우 느리고 과잉적합 우려
- 특징 벡터의 크기가 달라지면 연산 불가능
CNN
- 컨볼루션 연산을 이용한 부분연결(희소 연결) 구조로 복잡도를 크게 낮춤
- 컨볼루션 연산은 좋은 특징을 추출
- 가변 크기를 다룰 수 있다
- 컨볼루션층에서 보폭을 조정하거나 풀링층에서 커널이나 보폭을 조정하여 특징맵 크기 조절
CNN
- 격자 구조(영상, 음성 등)를 갖는 데이터에 적합
- 수용장(receptive field)은 인간시각과 유사
- 가변 크기의 입력 처리 가능
컨볼루션 연산
컨볼루션은 해당하는 요소끼리 곱하고 결과를 모두 더하는 선형 연산이다.
아래 식에서 \(u\)는 커널, \(z\)는 입력, \(s\)는 출력(특징 맵)이다.
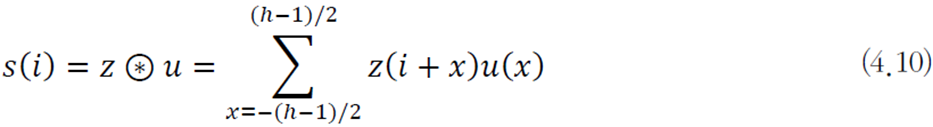
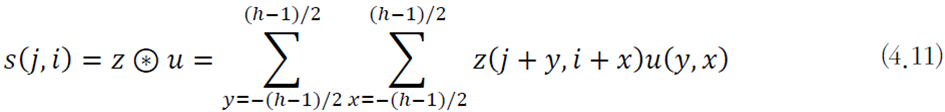
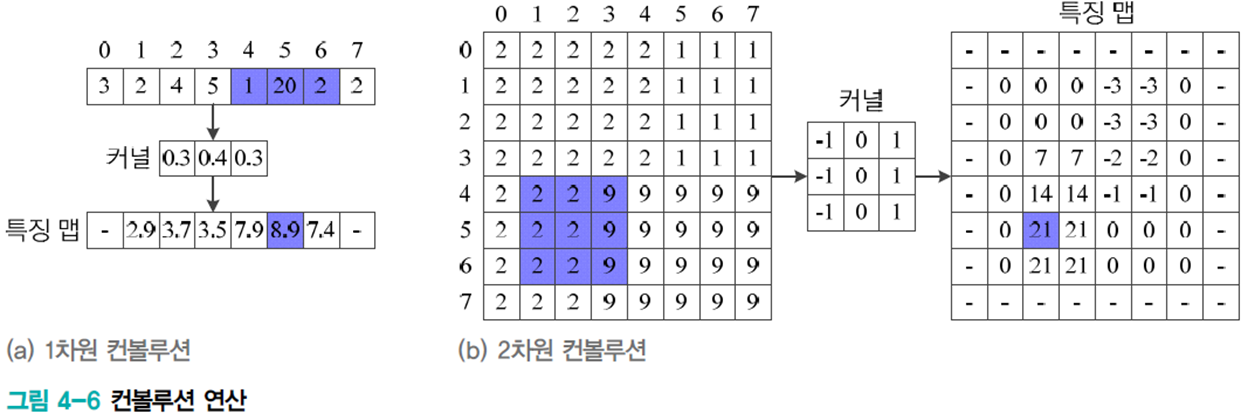
컨볼루션 연산에 따른 CNN 특성
- 이동에 동변 : 입력값이 이동해도 그대로 특징 맵에 반영된다. ex) 영상에서 물체 이동, 음성에서 발음 지연
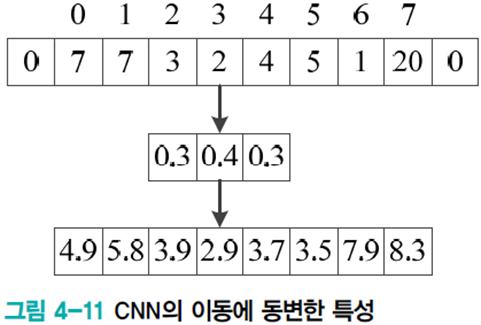
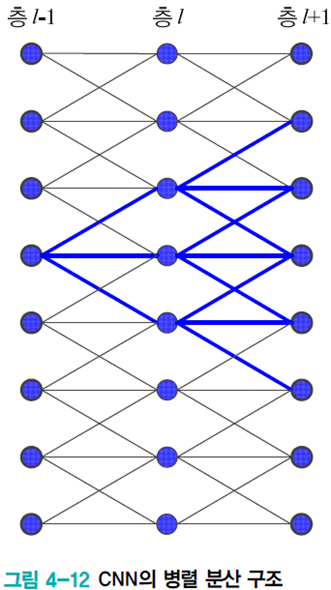
- 병렬 분산 구조
- 각 노드는 독립적으로 계산 가능한다. (GPU로 병렬 연산 가능)
- 오른쪽 그림과 같이 노드는 깊은 층을 거치면서 전체에 영향을 미친다.
컨볼루션 구조
덧대기(padding)을 통해 가장자리에서 영상의 크기가 줄어드는 효과를 방지한다.
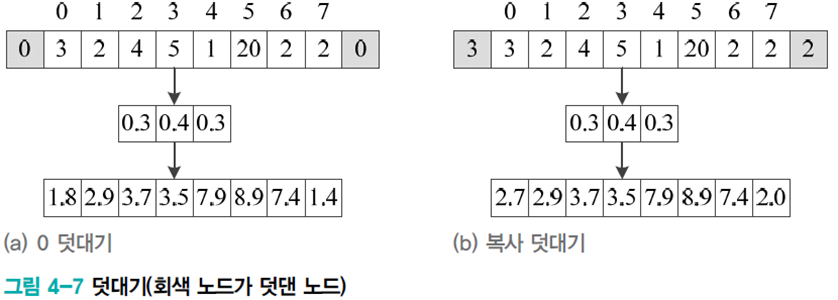
DMLP와 마찬가지로 바이어스를 주기도 한다.
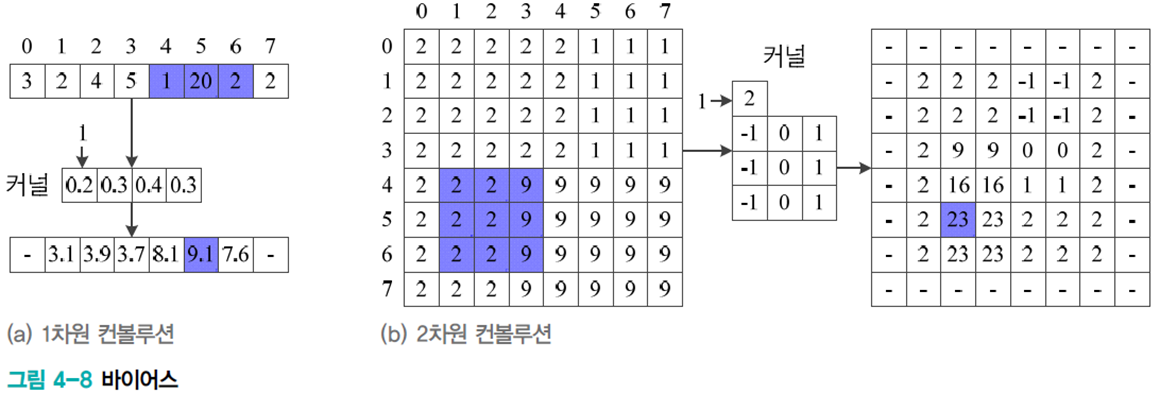
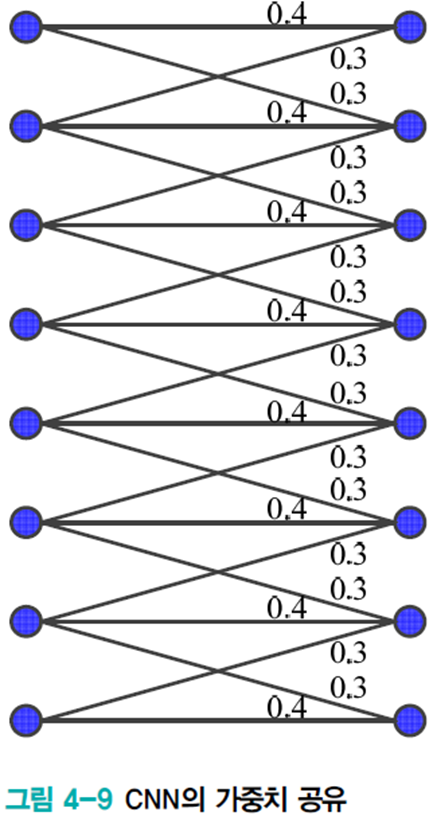
모든 노드는 같은 커널을 사용하여 가중치를 공유(weight sharing, tied weight)한다. 따라서 모델의 복잡도가 크게 낮아진다.
커널의 값에 따라 커널이 추출하는 특징이 달라지기 때문에 수십~수백 개 이상의 커널을 사용하여 특징을 추출한다.
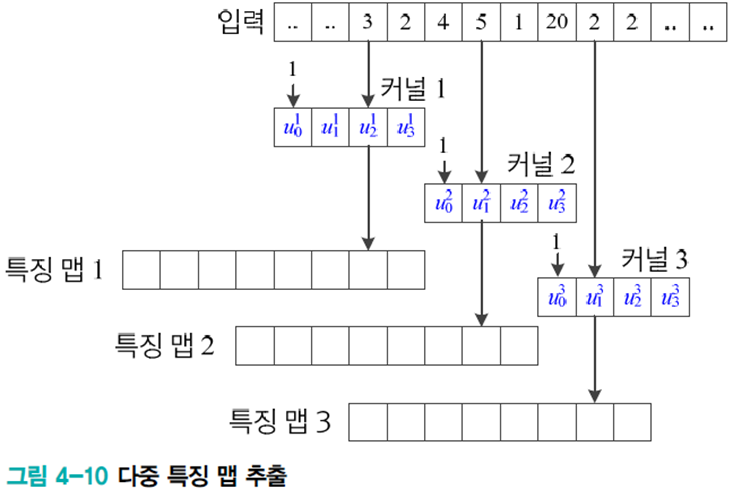
커널은 사람이 설계하지 않고 학습을 통해 알아낸다. 이 학습은 DMLP아 마찬가지로 오류 역전파로 커널을 학습한다.
\(u_{i}^{k}\)는 \(k\) 번째 커널의 \(i\) 번째 매개변수
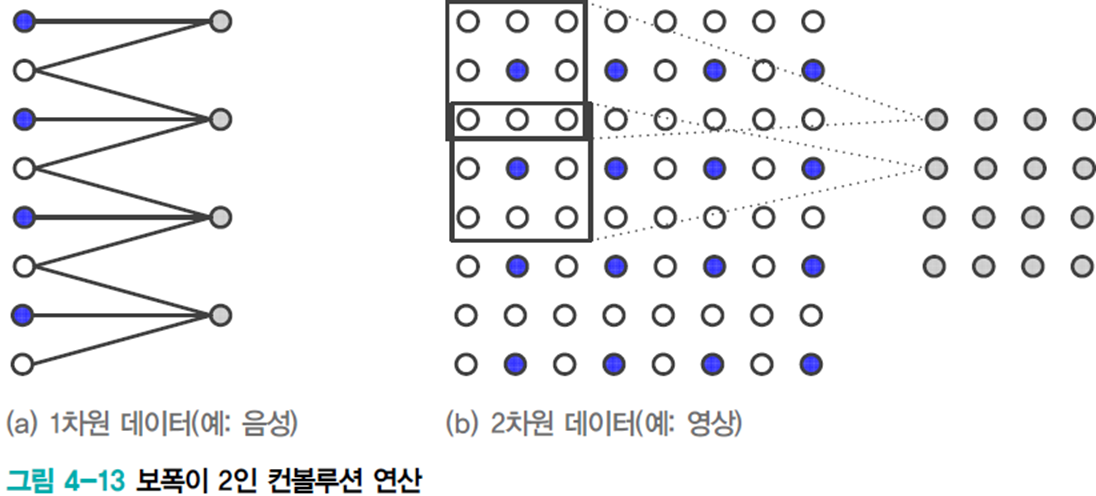
보폭(stride)의 크기를 조절하여 다운샘플링 크기를 조절한다.
일반적으로 보폭이 \(k\)이면 \(k\)개 마다 하나씩 샘플링하여 커널을 적용한다. 2차원 영상의 경우 특징 맵이 \(\frac{1}{k^{2}}\)로 작아진다.
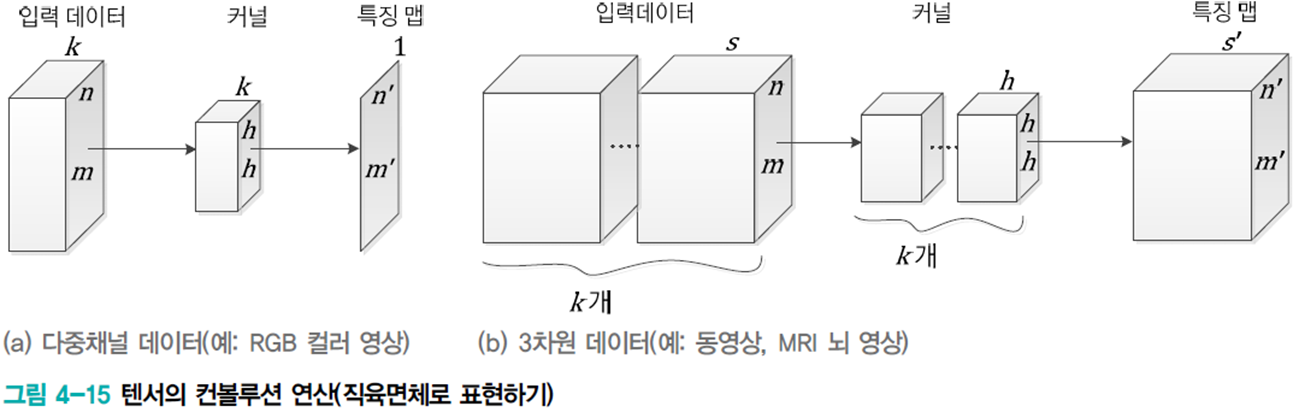
3차원 구조에서의 컨볼루션
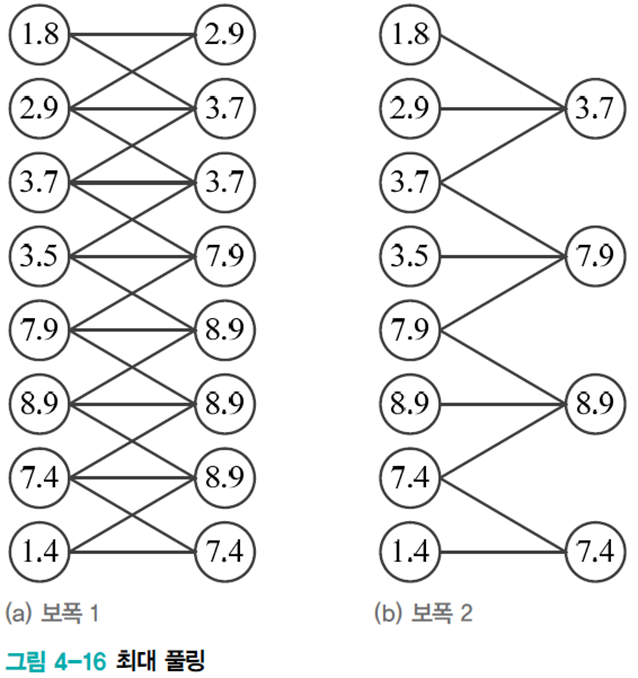
컨볼루션 연산이 만든 특징 맵은 노이즈를 포함한 상세한 정보가 담겨있는데 풀링은 상세 내용에서 디테일을 덜어낸 요약 통계를 추출한다. 매개변수가 없으며 특징 맵의 수를 그대로 유지한다.(보폭이 클 경우 다운샘플링 효과를 줌) 작은 이동에 둔감하여 물체 인식이나 영상 검색 등에 효과적이다.
CNN 전체 구조
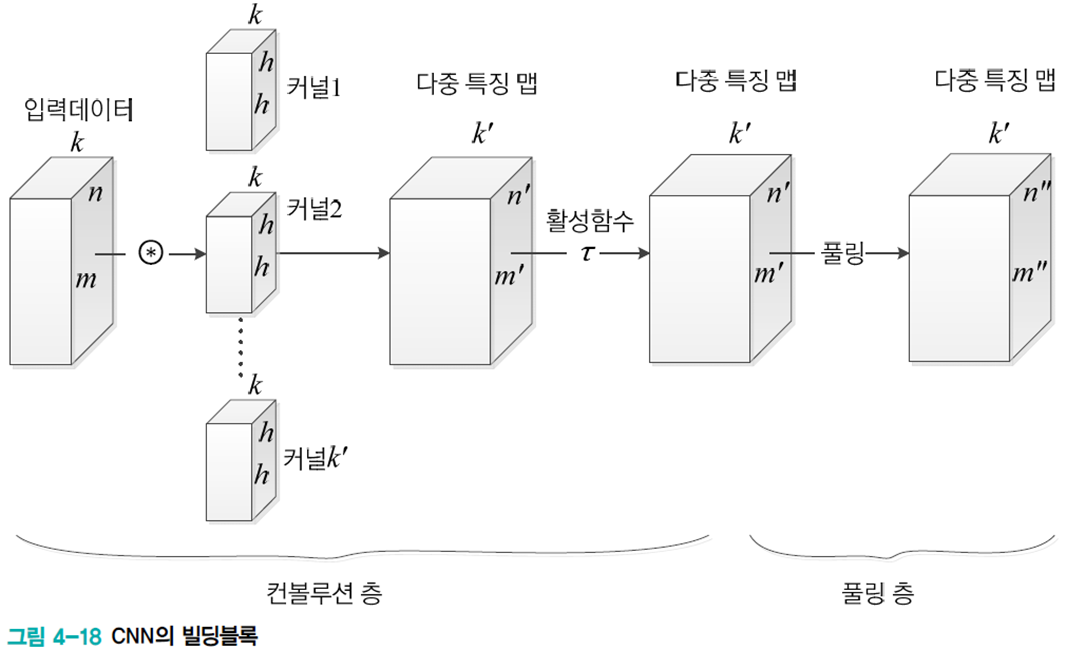
CNN은 빌딩블록을 이어 붙여 깊은 구조를 만든다. 전형적인 빌딩블록은 컨볼루션층 -> 활성함수(주로 ReLU) -> 풀링층의 구조를 갖는다. 다중 커널을 사용하여 다중 특징 맵을 추출한다.
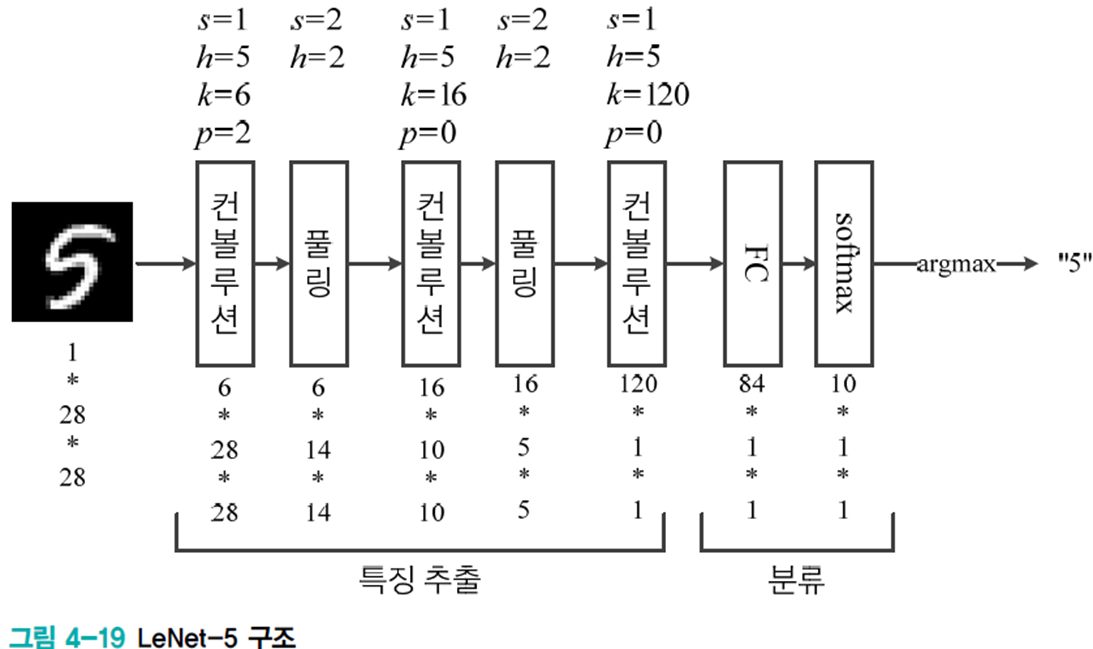
초창기 CNN 사례 LeNet-5, C(convolution)-P(pooling)-C-P-C의 다섯 층을 통해 특징 추출하고 은닉층이 하나인 MLP로 분류한다.
컨볼루션 신경망 사례연구
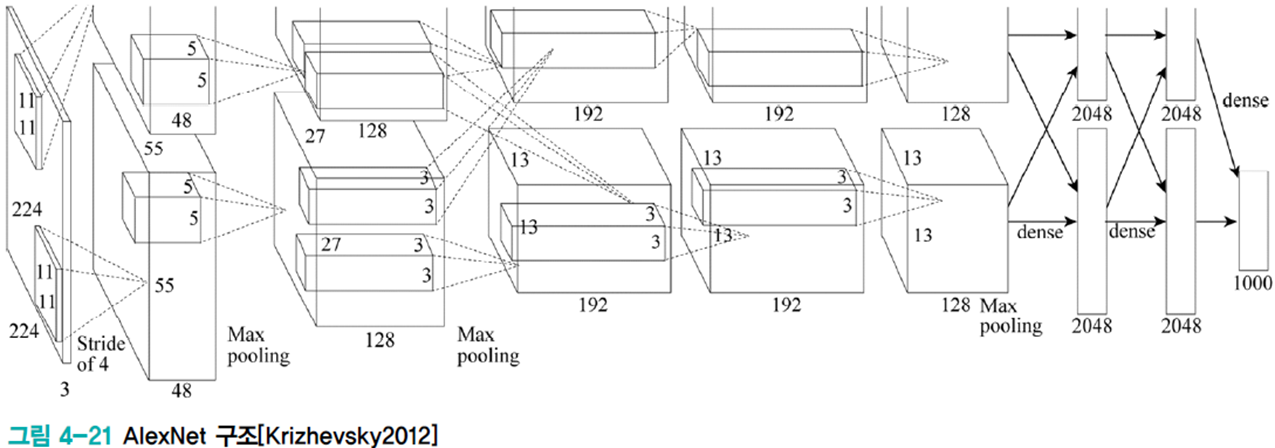
AlexNet
구조
파라미터가 컨볼루션층에서 200만개, FC층에서 6500만개 가량으로 FC층에서 30배 많은 매개변수를 사용한다. 향후 CNN은 FC층의 매개변수를 줄이는 방향으로 발전한다.
성공요인
- 외부 요인
- ImageNet이라는 대용량 데이터베이스
- GPU를 사용한 병렬처리
- 내부 요인
- 활성함수로 ReLU 사용
- 지역 반응 정규화 기법 적용
- 과잉적합을 방지하는 여러 규제 기법 적용
- 데이터 확대(크롭과 반전으로 데이터 크기를 2048배로 확대)
- 드롭아웃
- 테스트 단계에서의 앙상블로 2~3% 만큼 오류율 감소 효과
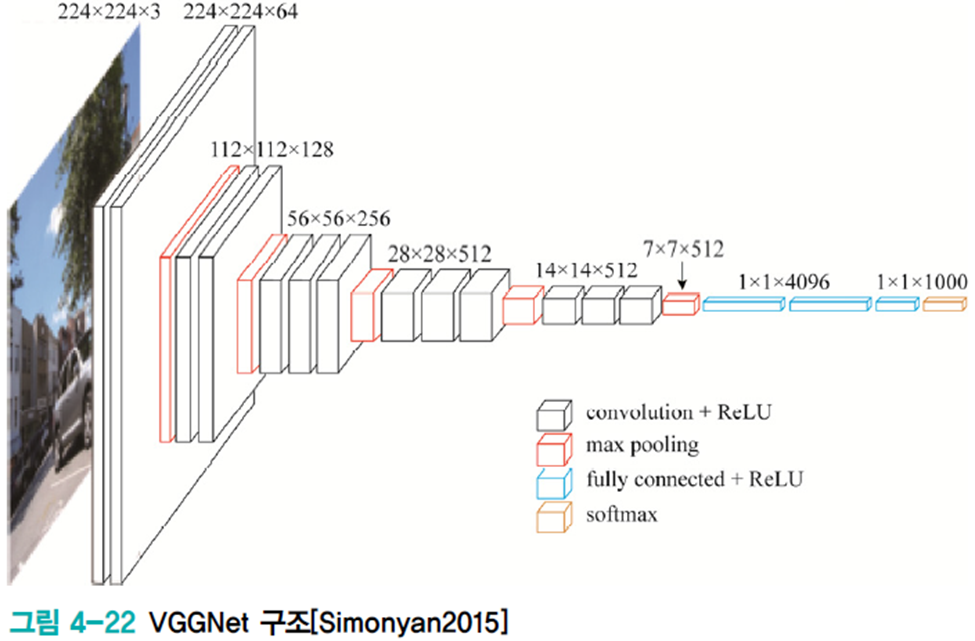
VGGNet
핵심 아이디어
커널사이즈를 3*3으로 작게 만드는 대신 신경망을 더욱 깊게 만들었다.
컨볼루션층을 8~16개를 두어 AlexNet의 5개에 비해 2~3배 깊어졌다.
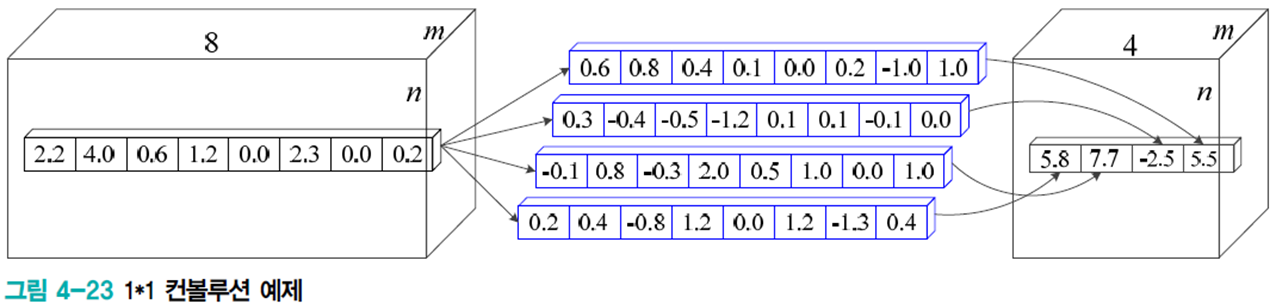
1*1 커널을 사용하였다. 이를 사용하면 다음의 효과를 얻는다. (다만 적용 실험만 하고 최종적으로 사용은 하지 않는다. 대신 GoogLeNet이 많이 사용한다.)
- 차원 축소 효과
- m*n의 특징 맵 8개에 1*1 커널을 4개 적용하면 m*n의 특징 맵 4개가 된다. 이는 다시말해 8*m*n 텐서에 8*1*1 커널을 4개 적용하여 4*m*n 텐서를 출력하는 셈이다.
- ReLU와 같은 비선형 활성함수를 적용하면 특징 맵의 분별력이 증가한다.
GoogLeNet
핵심 아이디어
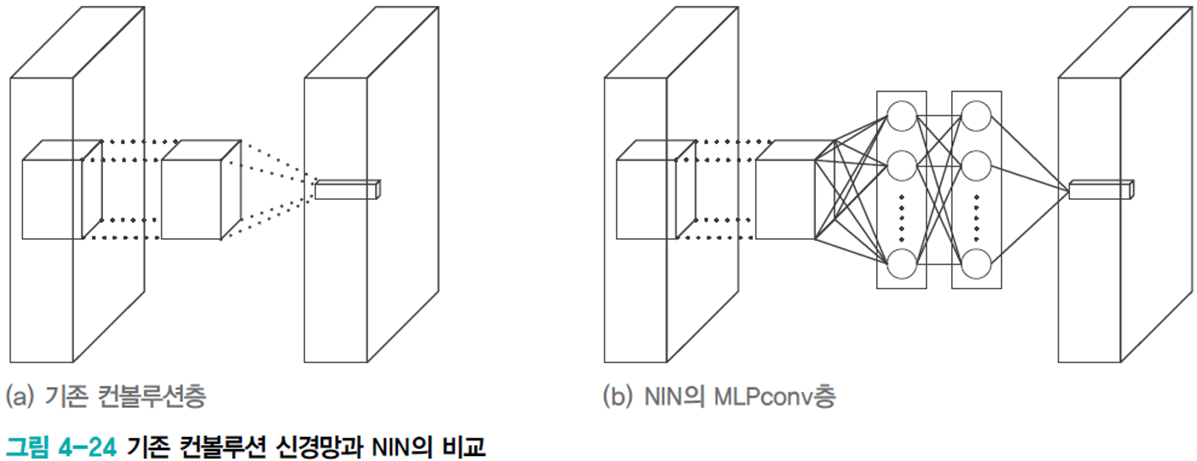
NIN 구조를 수정한 인셉션 모듈
NIN 구조
MLPconv 층이 컨볼루션 연산을 대신한다.
MLPconv는 커널을 옮겨가면서 MLP의 전방 계산을 수행한다.
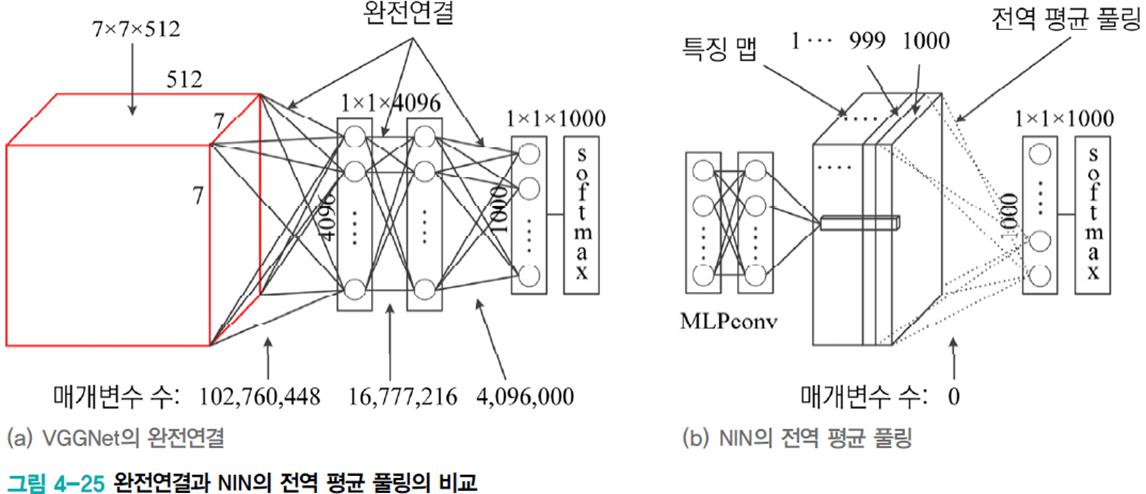
전역 평균 풀링(GAP)
아래 그림의 왼편은 VGGNet의 완전 연결층이다. 이는 VGGNet의 전체 매개변수의 85%를 차지하며 과잉적합의 원인이 된다.
따라서 NIN은 오른쪽 그림의 전역 평균 풀링을 사용하였다. MLPconv가 부류 수만큼 특징 맵을 생성하면, 특징 맵 각각을 평균하여 출력 노드에 입력하는 방식으로 매개변수를 없앴다.
GoogLeNet에선 이러한 NIN 구조를 아래와 같은 인셉션 모듈로 수정하여 다음 층에 4가지의 특징 맵을 전달하는 식으로 사용한다.
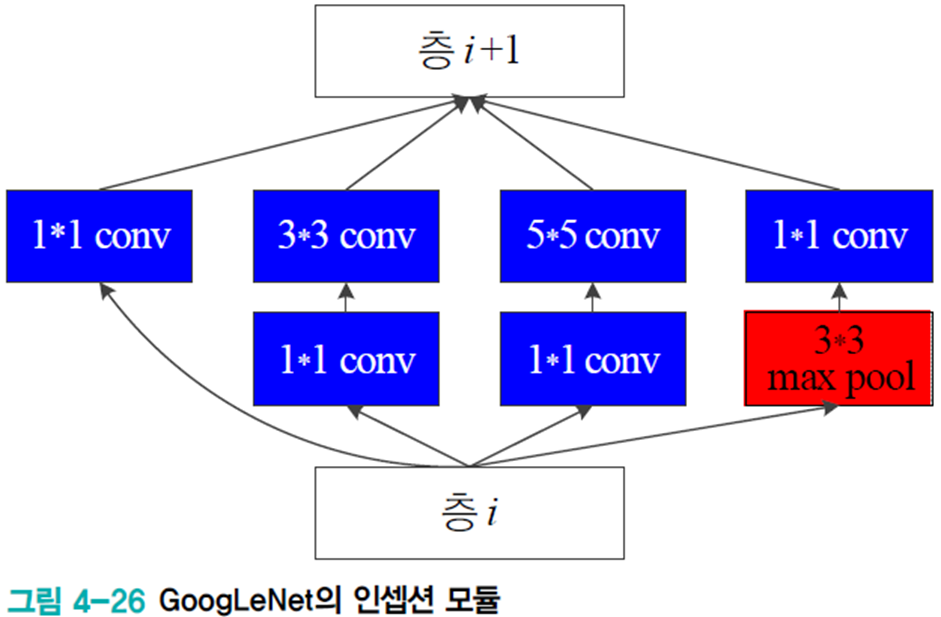
전체 구조는 다음과 같으며 인셉션 모듈을 9개 결합하여 매개변수가 있는 층은 22개, 없는 층은 5개로 총 27개의 층을 가지며 완전 연결층은 1개에 불과하여 1백만 개의 매개변수를 가진다. 이는 VGGNet의 완전연결의 1%에 불과하다.
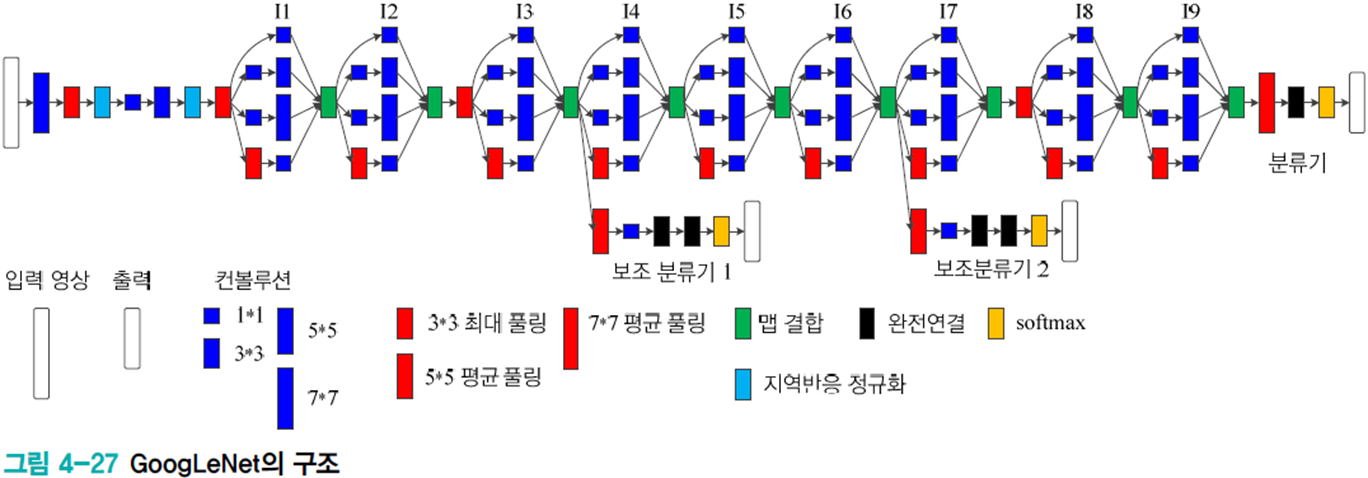
ResNet
잔류(residual) 학습이라는 아이디어를 이용하여 성능 저하를 피하면서 층 수를 대폭 늘렸다.(최대 1202층)
기존 컨볼루션 신경망은 다음과 같이 연산했다.
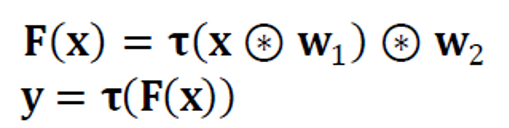
잔류 학습은 지름길(shortcut)이 연결된 x를 더한 F(x) + x에 \(\tau\)를 적용한다.
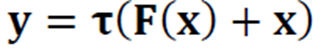
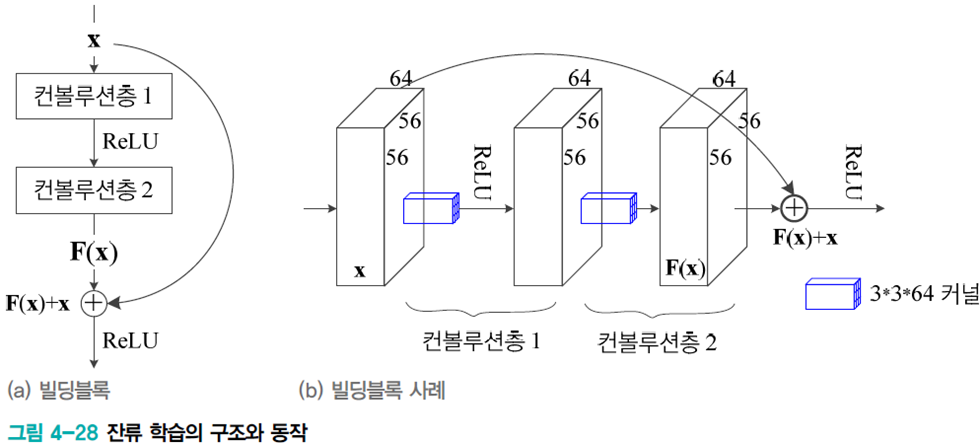
지름길 연결을 두는 이유
지름길 연결을 추가한 그레이디언트 계산식은 다음과 같다.
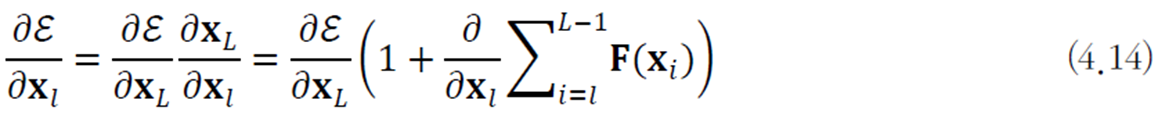
여기서 다음의 부분이 -1이 될 가능성은 거의 없으므로 그레이디언트 소멸 문제를 완화할 수 있다.
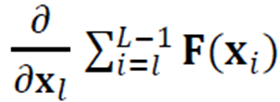
그렇기에 신경망 층을 매우 깊게 만들 수 있다.
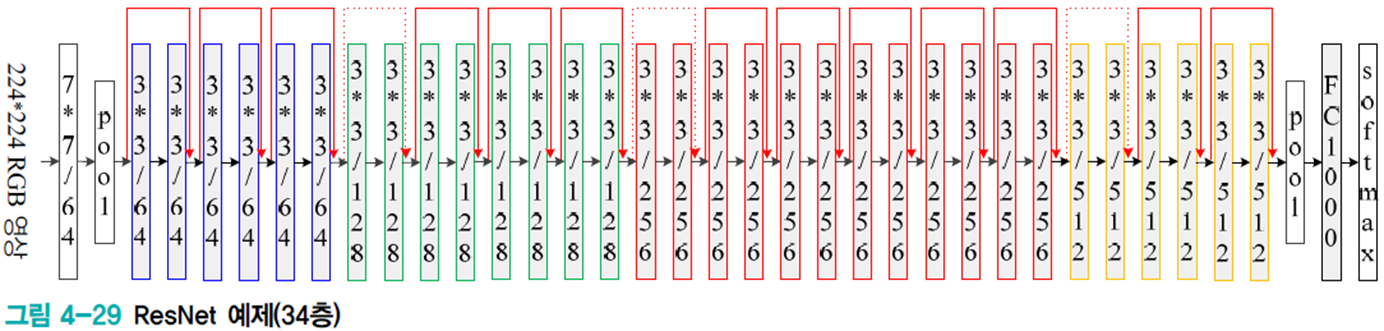
VGGNet와 같은 점은 3*3 커널을 사용했다는 점이다.
다른 점은 잔류 학습을 사용하고 전역 풀링을 사용하여 FC 층을 제거하고 배치 정규화를 적용(드롭아웃 적용 불필요)했다.
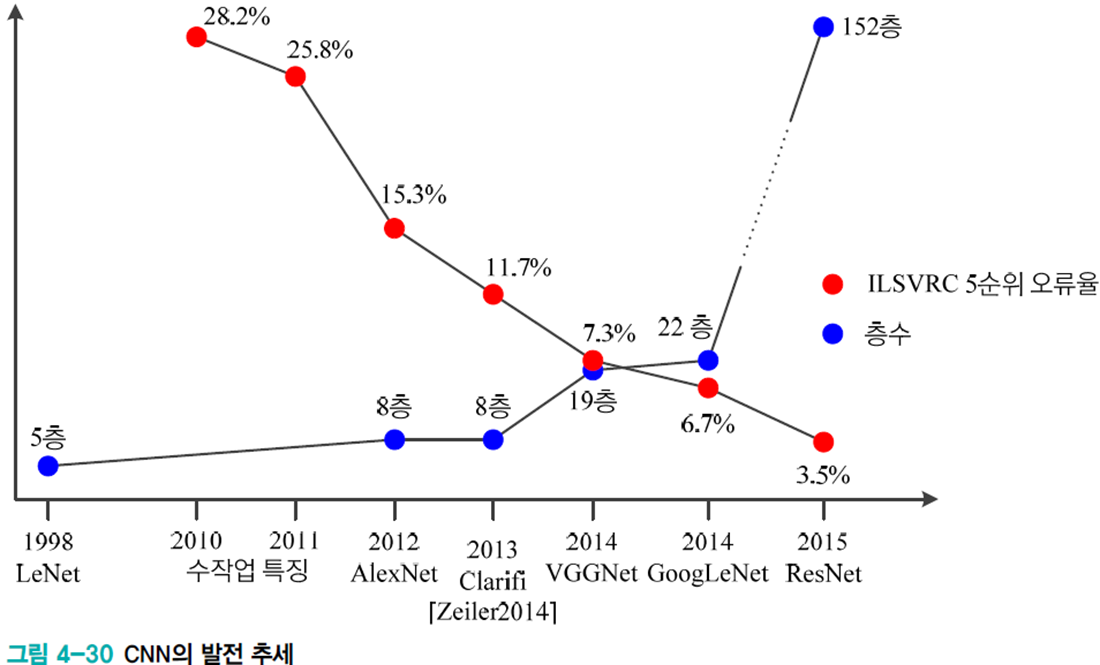
ILSVRC 대회에서 분류 문제는 성능이 포화(사람에 필적) 되었기 때문에 물체 검출 문제에 집중하고 있다.

GAN
생성 모델은 분별 모델에 비해 데이터 생성 과정에 대한 보다 깊은 이해를 필요로 한다.
분별 모델과 생성 모델의 비교

실제 상황에서의 생성 모델
자연계에 내재한 데이터 발생 분포 \(P_{data}(\textbf{x})\)를 알아낼 수 없다. 따라서 이를 모방하는 모델의 확률 분포 \(P_{model}(\textbf{x};\theta )\)를 구한다.
그러나 \(P_{model}(\textbf{x};\theta )\)를 명시적으로 추정하는 것도 불가능하기 때문에 현대 기계 학습은 주로 딥러닝 모델을 사용하여 확률 분포를 암시적으로 표현한다. ex) GAN, VAE, RNN, RBM
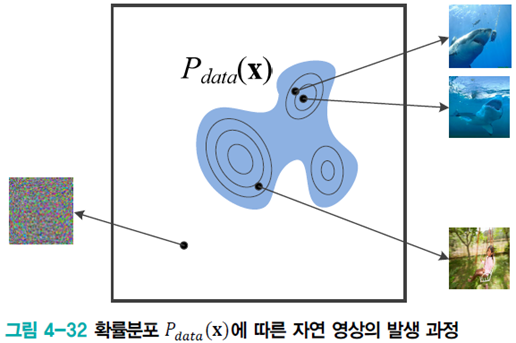
GAN은 사람을 상대로 진짜와 가짜를 구별하는 실험에서 MNIST는 52.4%, CIFAR-10은 78.7%로 MNIST의 경우 거의 완벽히 속일 정도로 우월한 성능을 보인다.

GAN의 아이디어
생성기 G와 분별기 D의 대립구도이다.
- G는 가짜 샘플을 생성한다.
- D는 가짜와 진짜를 구별한다.
GAN의 목표는 G가 만들어내는 샘플을 D가 구별하지 못하는 수준까지 학습하는 것이다.
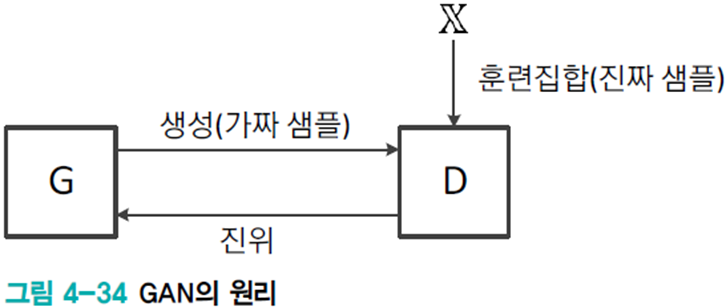
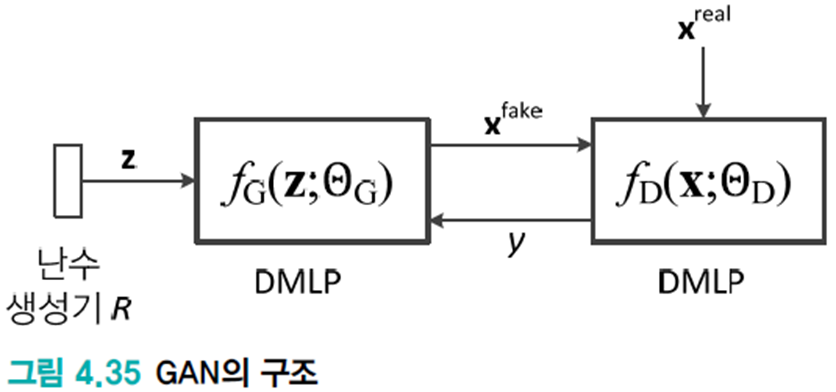
최초 GAN
G와 D를 DMLP로 구현하였다.
- G는 \(f_{G}(\textbf{z};\theta_{G})\), D는 \(f_{G}(\textbf{x};\theta_{G})\)로 표기한다.
- \(f_{G}\)는 난수 발생기로 만든 벡터 z를 입력으로 받아 가짜 영상을 출력한다.
- \(f_{D}\)는 영상을 입력으로 받아 진짜(1) 또는 가짜(0)를 출력한다.
GAN의 목적함수
목적함수 \(J_{D}\)와 \(J_{G}\)로 MSE 대신 로그우도를 사용한다.
분별기 D의 목적학수 \(J_{D}\)는 다음과 같다.
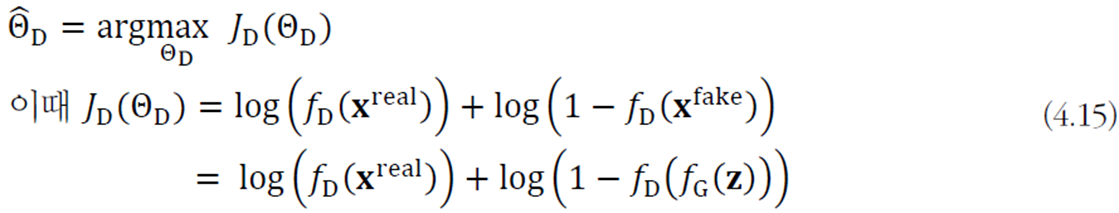
생성기 G의 목적함수 \(J_{G}\)는 다음과 같다.
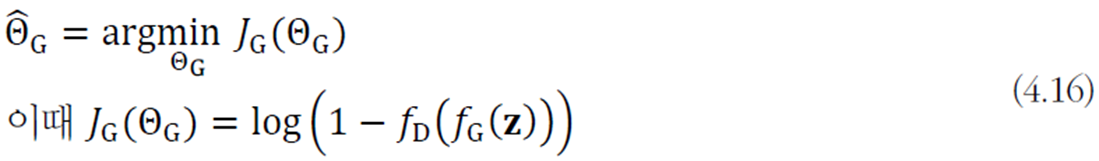
GAN의 학습 알고리즘은 다음과 같다.

개선된 GAN
Salimans2016에서 특징 매칭, 가상 배치 정규화, 미니배치 분별 등 여러 기법을 적용하고 \(P(\textbf{x})\) 대신 \(P(\textbf{x, y})를 추정하여 레이블이 있는 샘플을 생성하였다.
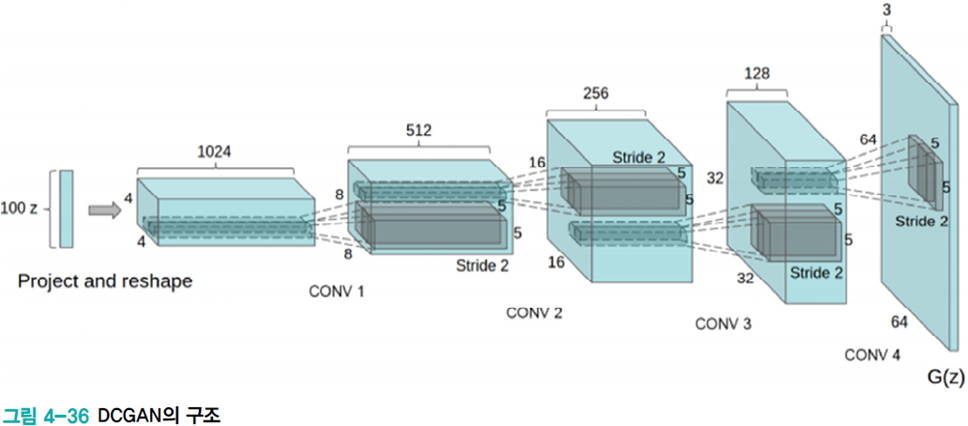
DCGAN(deep convolutional GAN)에서 DMLP 대신 CNN을 사용하였다. CNN과는 반대로 벡터를 입력받아 영상을 출력한다.
딥러닝이 강력한 이유
고전적인 방법에선 분할, 특징 추출, 분류를 따로 구현한 다음 이어붙인다. 이는 사람의 직관에 따르므로 성능에 한계가 있다. 또한 인식 대상이 달라지면 새로 설계해야 한다.
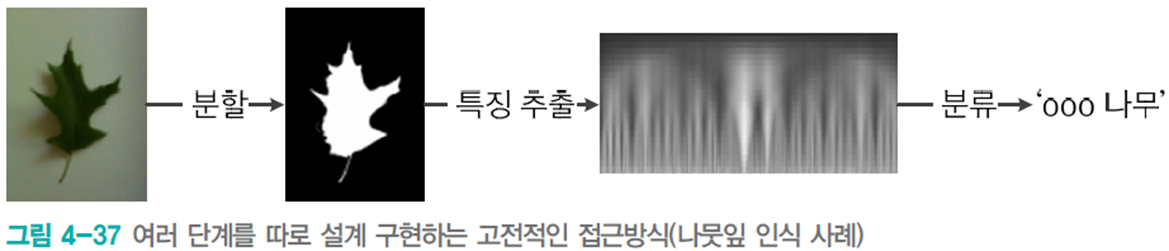
딥러닝은 end-to-end로 전체 과정을 동시에 최적화한다.
딥러닝에서 깊이의 중요성
층이 더 깊을수록 더 정교한 분할을 한다.
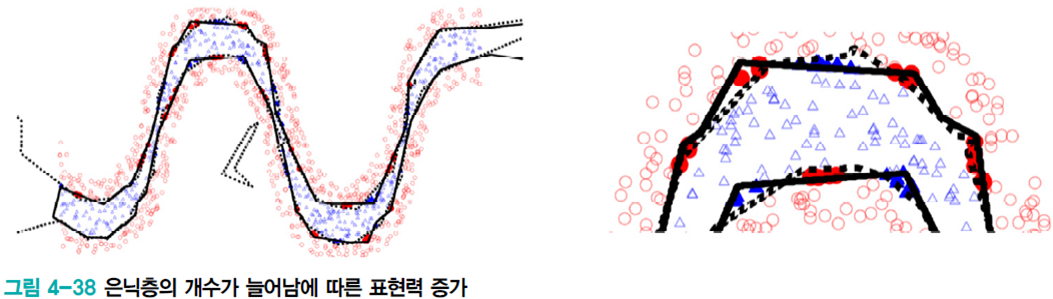
계층적 특징
깊은 신경망에선 층마다의 역할이 잘 구분된다. 반면에 얕은 신경망은 하나 또는 두 개의 은닉층이 여러 형태의 특징을 모두 담당하기에 깊은 신경망이 성능면에서 더 유리하다.
'공부한 내용 정리 > 인공지능' 카테고리의 다른 글
| 인공지능 기초 4 (1) | 2023.03.25 |
|---|---|
| 인공지능 기초 3 (0) | 2023.03.20 |
| [논문 리뷰]Latent Aspect Rating Analysis on Review Text Data:A Rating Regression Approach (0) | 2023.02.27 |
| 인공지능 기초 1 (0) | 2023.02.24 |
| [논문 리뷰]EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks (0) | 2023.02.07 |
