티스토리 뷰
들어가며
본 게시물은 오일석 교수님의 기계학습 강의 6장을 보고 정리한 글입니다.
비지도학습
앞서 배웠던 학습 방법은 지도학습으로 훈련집합
반면 비지도학습에선
이는 맞춤 광고, 차원 축소, 데이터 압축, 데이터 가시화, 특징 추출, 생성 모델 등 여러 분야에서 응용된다.
특징 추출의 특성 때문에 현대 기계학습에서 더욱 중요해졌다.
지도 학습, 비지도 학습, 준지도 학습 비교
- 지도 학습 : 모든 훈련 샘플이 레이블 정보를 갖는다.
- 비지도 학습 : 모든 훈련 샘플이 레이블 정보를 갖지 않는다.
- 준지도 학습 : 레이블을 가진 샘플과 가지지 않은 샘플이 섞여있다.

기계학습에선 크게 두 가지 지식이 주어진다고 볼 수 있다.
훈련집합 : 데이터를 수집하여 구성한 것
사전 지식(prior knowledge) : 세상의 일반적인 규칙
사전 지식
매니폴드 가정(manifold hypothesis)
패턴이 고차원 공간에서 매니폴드라 불리우는 저차원 분포로 구성되어 있다는 가정이다.
데이터집합은 하나의 매니폴드 또는 여러 개의 매니폴드를 구성하며, 모든 샘플은 매니폴드와 가까운 곳에 있다.
MNIST를 예로 들면 숫자, 획의 끊김 등 이러한 변화를 축으로 가정하면 수십 개 정도의 변화가 있고, 샘플들이 수십차원의 낮은 차원의 공간에 존재한다는 것이다.
매끄러움 가정(smoothness hypothesis)
샘플이 어떤 요인에 의해 변화한다는 것이다.
비지도 학습과 준지도 학습은 지도학습에 비해 이러한 사전지식을 더 활용한다.
비지도 학습의 일반 과업
- 군집화 : 유사한 샘플을 모아 같은 그룹으로 묶는 일
- 맞춤 광고, 영상 분할, 유전자 데이터 분석, SNS 실시간 검색어 분석 등 여러 응용분야가 있다.
- 밀도 추정 : 데이터로부터 확률분포를 추정하는 일
- 분류, 생성 모델 구축 등의 응용 분야가 있다.
- 공간 변환 : 원래 특징 공간을 저차원 또는 고차원으로 변환하는
- 데이터 가시화, 데이터 압축, 특징 추출(표현 학습) 등의 응용 분야가 있다.
데이터에 내재한 구조를 잘 파악하여 새로운 정보를 발견해야 한다.

군집화
군집화 문제

군집의 개수
군집화를 부류 발견 작업이라 부르기도 한다.
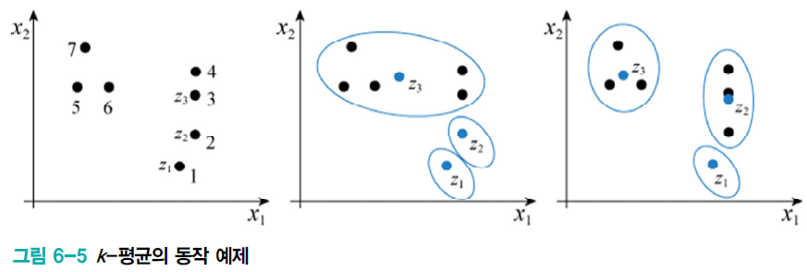
군집화는 주관적이다. 아래 그림처럼 정답은 없고 주관적이다.

원리는 단순하지만 성능이 좋아 인기가 좋다.
직관적으로 이해하기 쉽고 구현이 쉽다.
군집 개수

군집 중심은 랜덤하게 초기화하거나 사전 정보가 있으면 그에 따라 선택한다.

행렬
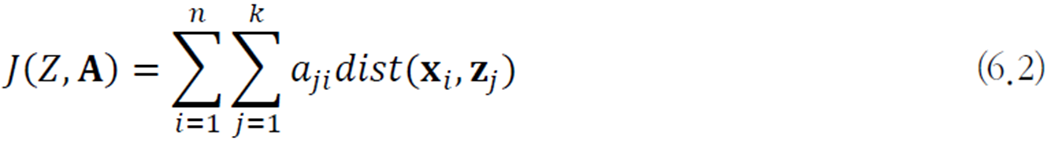
다중 시작

- 중간 단계의 임시 변수
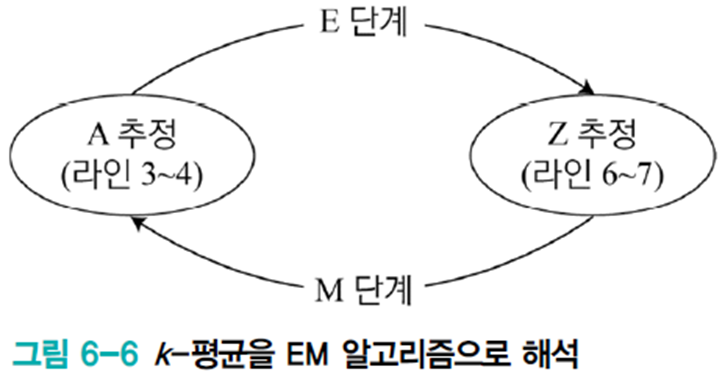
굳이 이를 EM으로 해석하는 이유는 추후 복잡한 EM 형태의 알고리즘을 이해하는데 도움이 되기 때문이다.
친밀도 전파 알고리즘
비교적 최근 나온 알고리즘이다.
책임 행렬
군집 개수
샘플
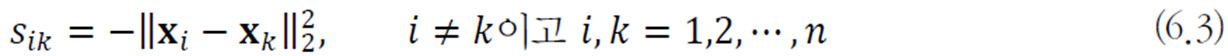
여기서 거리를 구할 때 문제에 따라 유클리드 거리 외에 다른 것을 정의하기도 한다.
책임 행렬

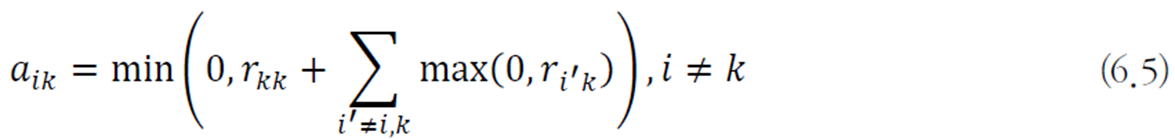
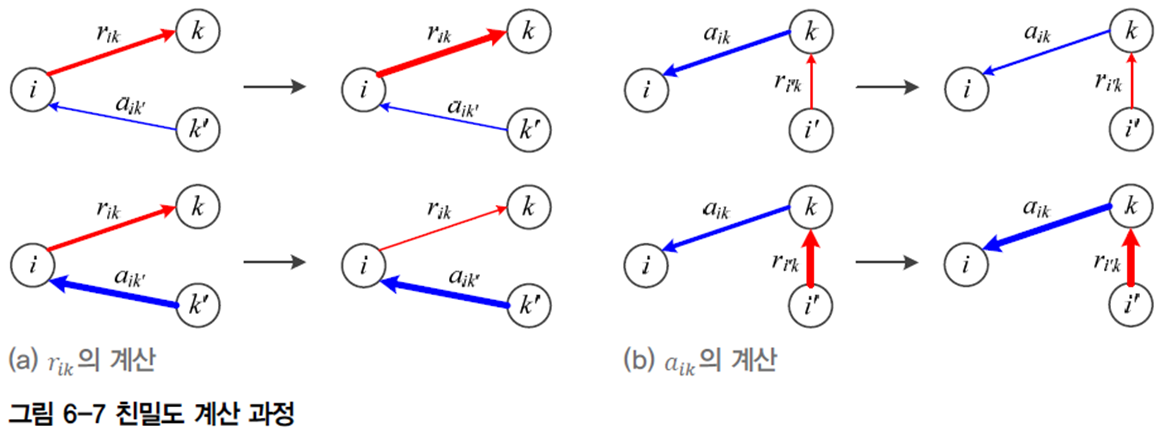
하이퍼 파라미터로 자가 유사도
유사도의 최솟값, 중앙값, 최댓값 중에 선택하며 최솟값은 적은 수의 군집, 최댓값은 많은 수의 군집, 중앙값은 중간 정도의 군집을 의미한다.
자가 친밀도는 다음과 같이 계산된다.
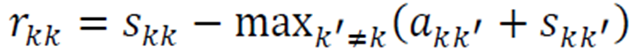
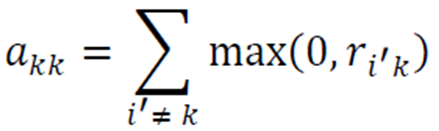
위의 요소들을 조합하여 알고리즘을 구성하면 다음과 같다.

밀도 추정
어떤 점
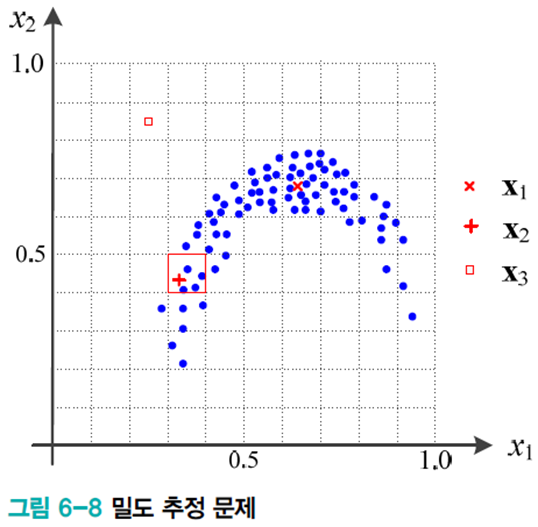
커널 밀도 추정
히스토그램 방법
위 그림과 같이 특징 공간을 칸의 집합으로 분할한 다음, 칸에 있는 샘플의 빈도를 세어 다음 식으로 추정한다.

여기서
그러나 이 방법은 매끄럽지 못하고 계단 모양을 띠는 확률 밀도함수가 된다. 또한 칸의 크기와 위치에 민감하다.
커널 밀도 추정법
점
다음 식에선 대역폭
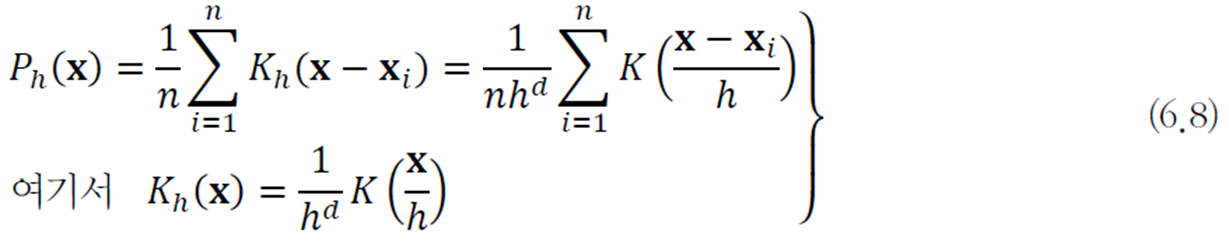
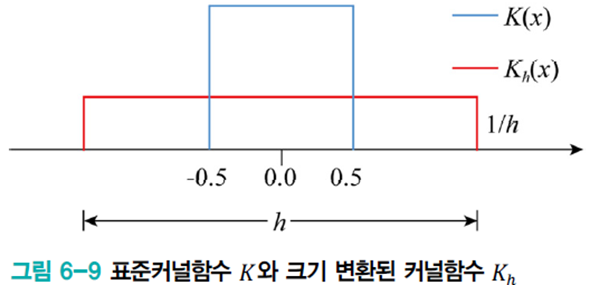
히스토그램 방법과 커널 밀도 추정법을 비교해 봤을 때 커널 밀도 추정법이 매끄러운 확률밀도함수를 추정함을 알 수 있다.
다음 그림은 대역폭
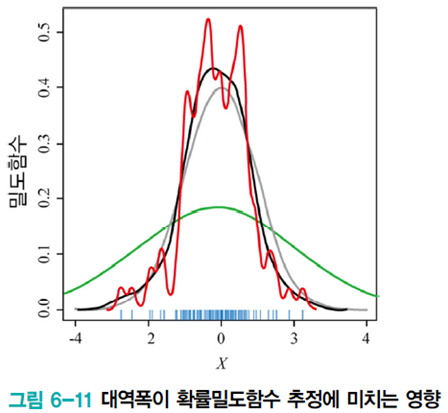
그러나 커널 밀도 추정 기법의 근본적인 문제점이 있다.
- 샘플을 모두 저장하고 있으며 매번 새로운 샘플이 주어질때마다 처음부터 다시 계산해야 된다.(메모리 기반 방법)
- 차원의 저주에 취약하다. 따라서 데이터가 낮은 차원인 경우로 국한하여 활용한다.
가우시안 혼합
이 방법은 데이터가 높은 차원일 경우에도 적용이 가능하다.
이는 가우시안을 이용한 모수적 방법이다. 데이터가 가우시안 분포를 따른다고 가정하고 평균 벡터
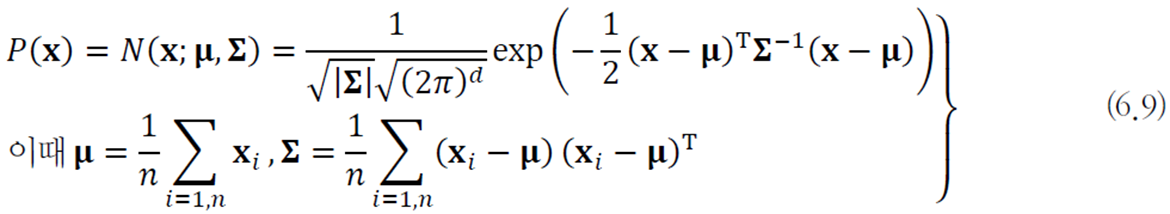
대부분의 데이터가 오른쪽 그림과 같이 하나의 가우시안으로 데이터 구조를 반영하기엔 불충분하다.
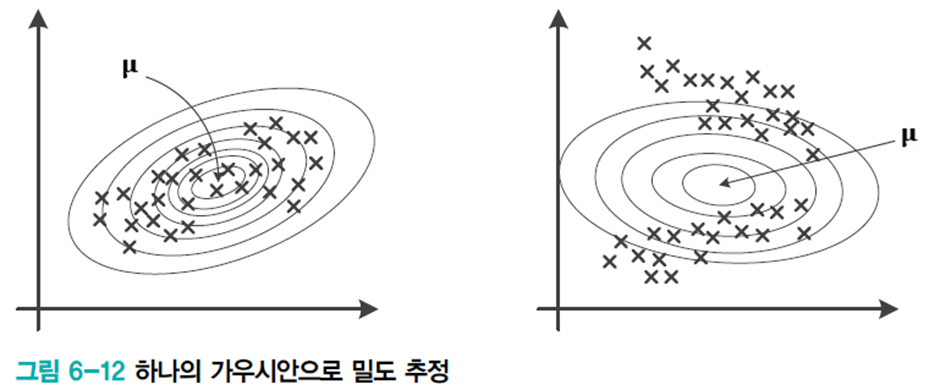
따라서 여러개의 가우시안을 사용하여 데이터 구조를 표현한다. 이를 가우시안 혼합이라 한다.

가우시안 혼합에서 주어진 데이터와 추정해야 할 매개변수를 정리하면 다음과 같다.
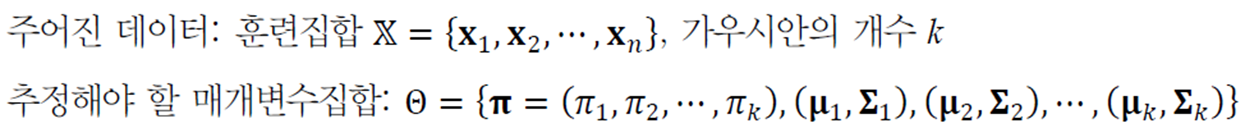
이를 최대 우도를 이용한 최적화 문제로 공식화하면 다음과 같다.
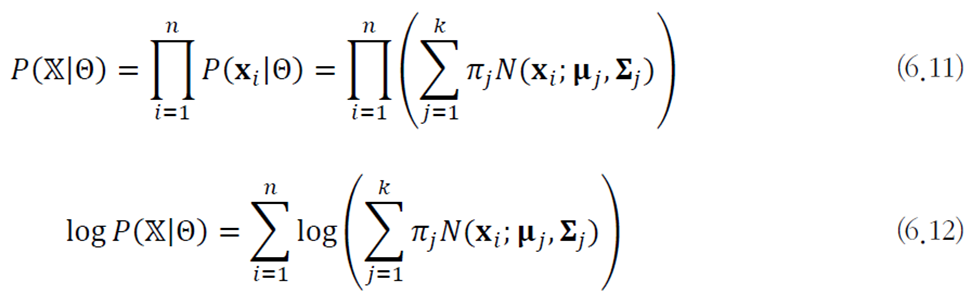

이 최적화 문제를 풀기 위해 EM 알고리즘을 적용한다.
처음엔
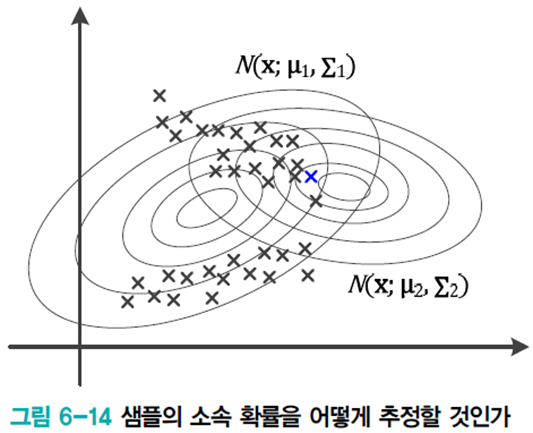
이를 EM으로 개선한다.
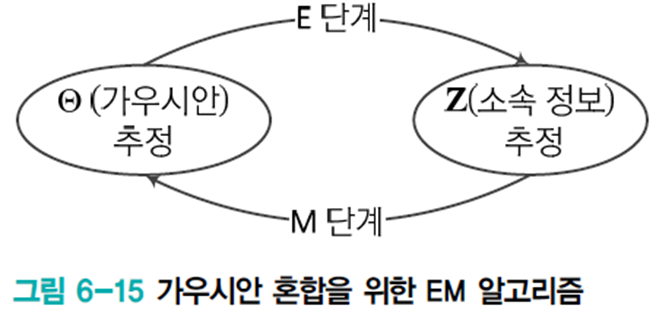
가우시안 샘플의 소속 정보 개선(E 단계) -> 샘플의 소속 정보로 가우시안 개선(M 단계) -> ... 이 과정을 반복한다. 여기서 소속 정보는
이를 알고리즘화 하면 다음과 같다.

3, 4번 줄을 수식화하면 다음과 같다.
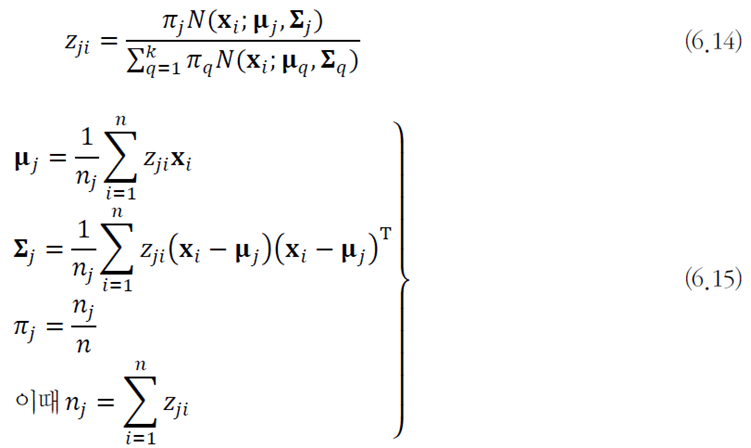
공간 변환
예시) 극좌표를
실제 문제에서는 비지도 학습을 이용하여 최적의 공간 변환을 자동으로 알아내야 한다.
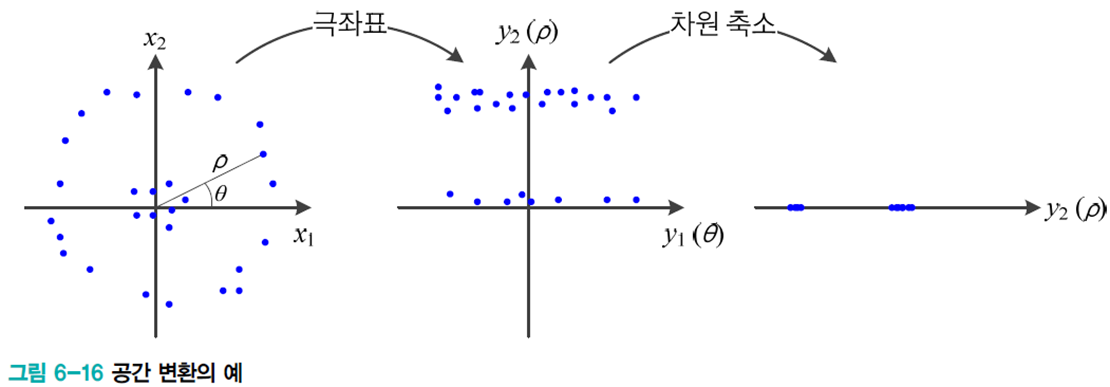
인코딩과 디코딩
원래 공간을 다른 공간으로 변환하는 인코딩과정(
데이터 압축의 경우 역변환으로 얻은
데이터 가시화에서는 2차원 또는 3차원의
선형 인자 모델
선형 연산을 이용한 공간 변환 기법이다.
선형 연산을 사용하므로 행렬 곱으로 인코딩과 디코딩 과정을 표현한다.

이 식에서
인자
주성분 분석(PCA)
주성분 분석은 처음 단계로 데이터를 원점 중심으로 옮기는 전처리를 먼저 수행한다.
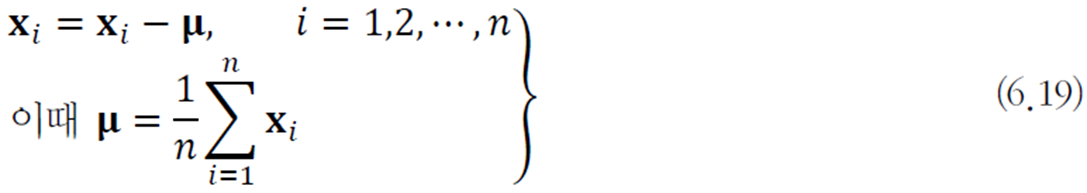
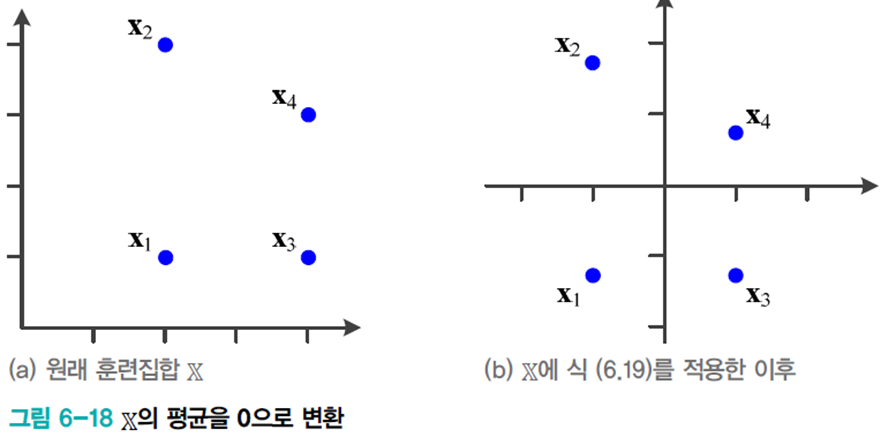
변환 행렬
이때
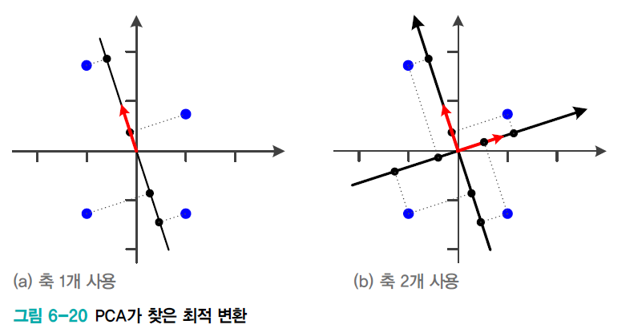
아래 그림은 2차원을 1차원으로 변환하는 상황이다.(
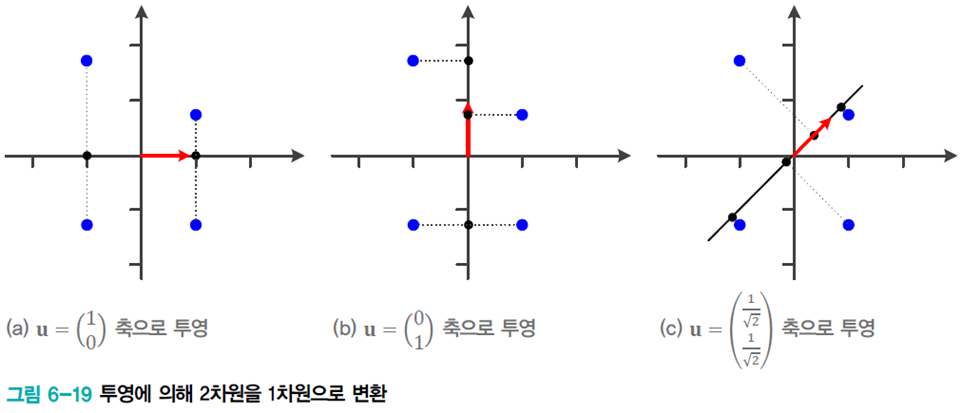
주성분 분석의 목적은 손실을 최소화하면서 저차원으로 변환하는 것이다. 위 그림의 경우 1, 2 번째는 각 축에서 같은 점으로 변환되는 정보 손실이 발생하지만 3 번째 그림은 4개 점 모두 다른 점으로 변환되어 정보 손실이 가장 적다.
주성분 분석은 변환된 훈련집합
PCA는 최적화 문제로 다음과 같이 정의할 수 있다.

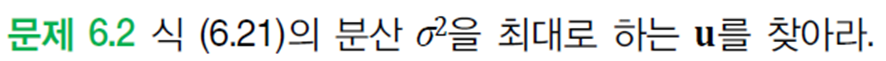
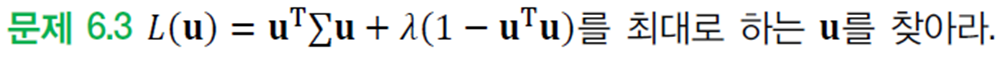
최적해는 미분으로 다음과 같이 구한다.

이 점을 갖고 주성분 분석의 학습 알고리즘을 서술하면 다음과 같다.
- 훈련집합으로 공분산 행렬
- 고윳값이 큰 순서대로
독립 성분 분석(ICA)
대표적인 예시론 블라인드 원음 분리 문제이다. 실제 세계에서는 악기 연주소리와 사람 대화소리와 같이 여러 신호가 섞여 나타난다.
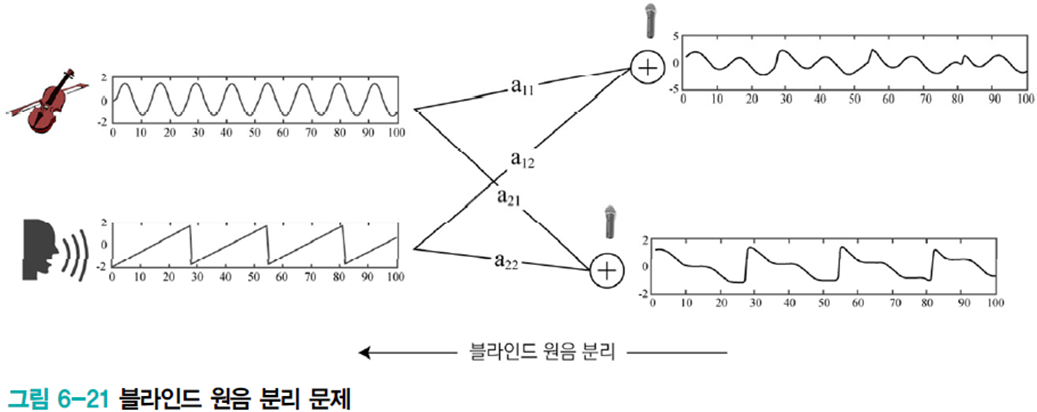
마이크로 측정한 혼합 신호로부터 원음을 복원할 수 있는지에 대한 물음을 블라인드 원음 분리 문제라 부르며 이는 독립 성분 분석 기법으로 해결 가능하다.
문제를 정의해보자.
원래 신호를
이 블라인드 원음 분리 문제는
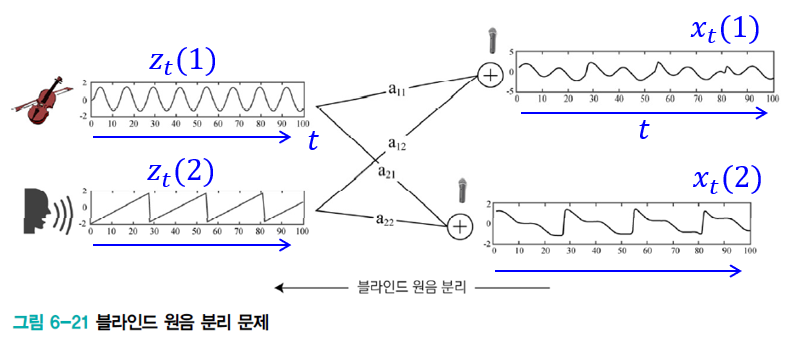
문제 공식화

행렬 표기론 다음과 같다.

블라인드 원음 분리 문제란

그러나 (6.25)는 과소 조건 문제이다. 따라서 유일 해를 얻기엔 조건이 부족하다. 그렇기에 추가 조건을 이용하여 해를 찾는다. (독립성 가정과 비가우시안 가정)
독립성 가정
원래 신호가 서로 독립이라는 가정
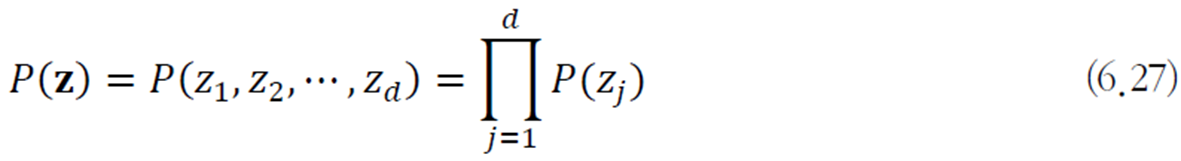
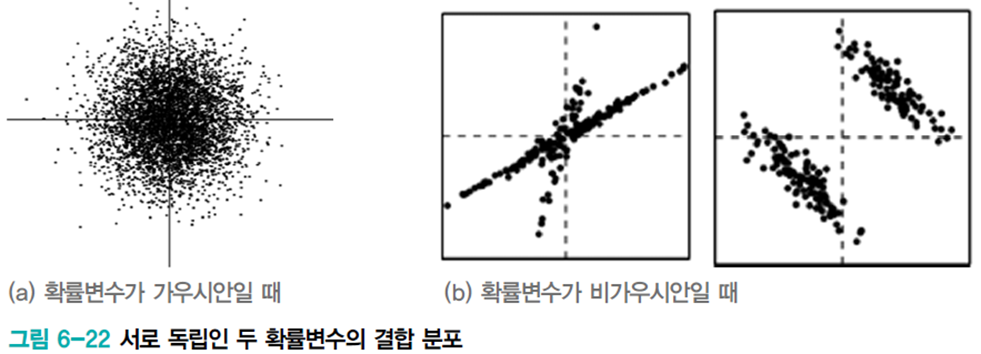
비가우시안 가정
원래 신호가 가우시안이라면 혼합 신호도 가우시안이 되므로 분리할 수 없다. 만약 비가우시안이면 오른쪽 그림처럼 분리할 실마리가 있다.
ICA의 문제 풀이
원래 신호의 비가우시안 정도를 최대화하는 가중치를 구하는 전략을 사용한다.
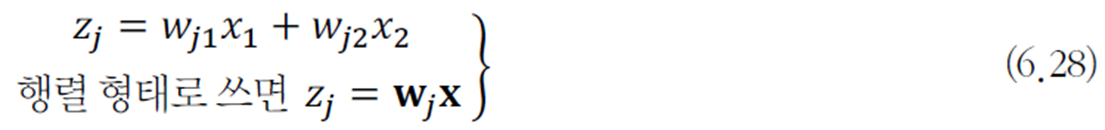
비가우시안을 최대화하는 가중치를 구하는 식은 다음과 같다.
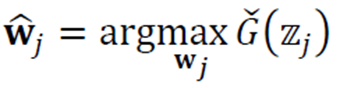
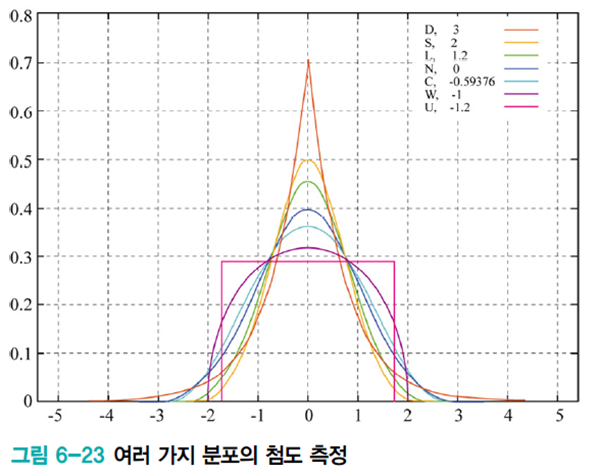
G는 비가우시안 정도를 측정하는 함수이며 주로 첨도를 사용한다.
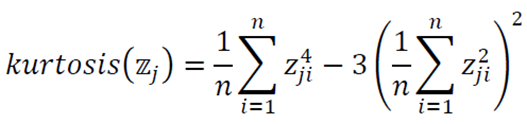
위 식은 다음의 전처리를 수행한 다음 적용한다.
훈련집합
다음의 화이트닝 변환 적용 (공분산 행렬을 단위행렬로 만들어버려 유클리디안 거리를 통해 쉽게 거리를 측정할 수 있도록 함)
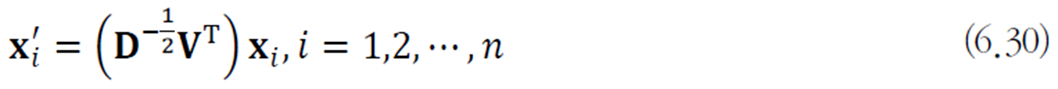
PCA와 ICA의 비교
- ICA는 비가우시안과 독립성 가정, PCA는 가우시안과 비상관을 가정한다.
- ICA는 4차 모멘트까지 사용, PCA는 2차 모멘트까지 사용한다.
- ※ 모멘트란 어떤 종류의 물리적 효과가 하나의 물리량뿐만 아니라 그 물리량의 분포 상태에서 따라서 정해질때에 정의되는 양. 0차는 PDF의 면적, 1차는 평균, 2차는 분산, 3차는 비틀림, 4차는 첨도를 의
- ICA로 찾은 축은 수직이 아니나 PCA로 찾은 축은 서로 수직이다.
- ICA는 주로 블라인드 원음 분리와 같은 문제를 푸는데, PCA는 차원 축소 문제를 푼다.
희소 코딩
예전부터 공학수학에선 푸리에 변환이나 웨이블릿 변환과 같이 기저함수 또는 기저 벡터의 선형 결합으로 신호를 표현해왔다.
희소 코딩은 오른쪽 그림과 같이 사전

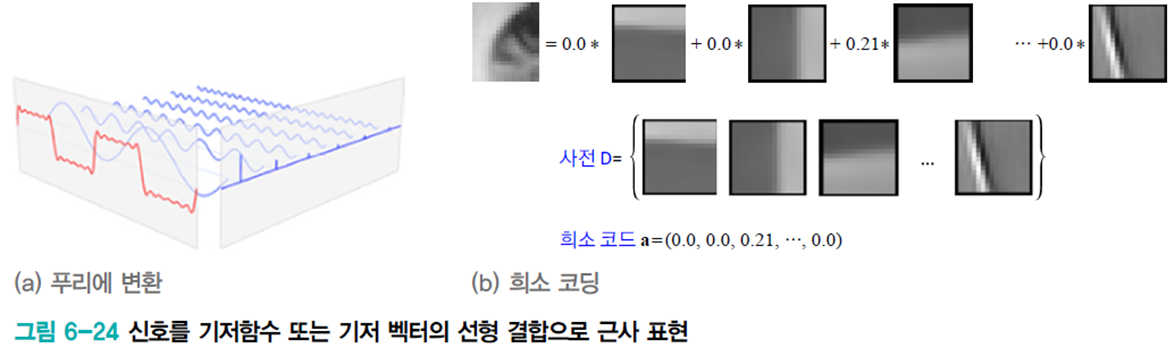
희소 코딩이 다른 변환 기법과 다른 점이 몇 가지 있다.
- 희소 코딩에선 비지도 학습이 사전(기저 벡터)를 자동으로 알아낸다. (푸리에 변환에선 삼각함수) 즉, 희소 코딩은 데이터에 맞는 기저 벡터를 사용하는 셈이다.
- 사전의 크기를 차원에 비해 크게 책정한다.
- 희소 코드
희소 코딩은 다음 식으로 구현될 수 있다. 딕셔너리와 희소 코드의 곱이 자기 자신과 최대한 갖게 만들며
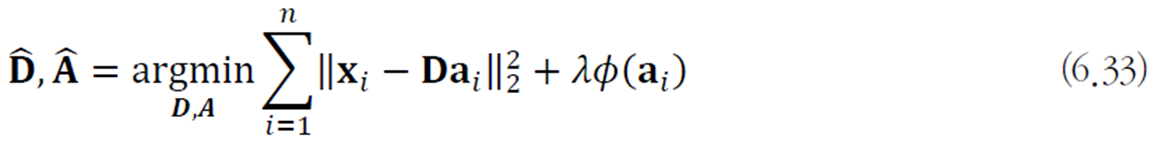
오토인코더
특징 벡터
병목 구조 오토인코더의 동작 원리
은닉층의 h는 훨씬 적은 메모리로 데이터를 표현하고 필요하다면 디코더로 원래 데이터를 복원한다.
h는 x의 핵심 정보를 표현한다. 이는 특징 추출, 영상 압축 등에 응용될 수 있다.
활성함수에 따라 선형과 비선형으로 나뉜다.
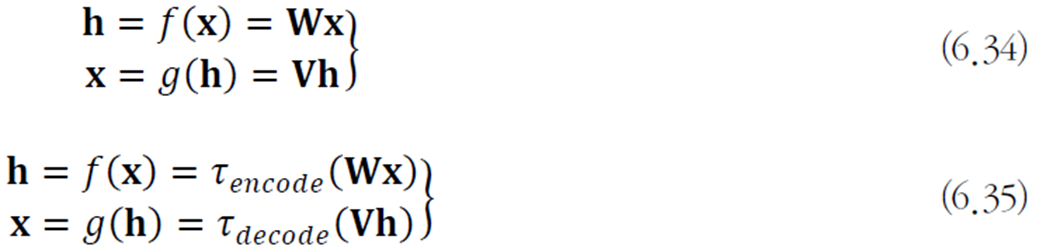
오토인코더의 학습
주어진 데이터는 훈련집합
최적화 문제로 쓰면 다음과 같다.
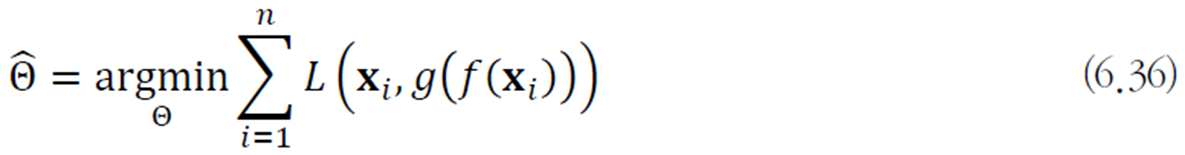
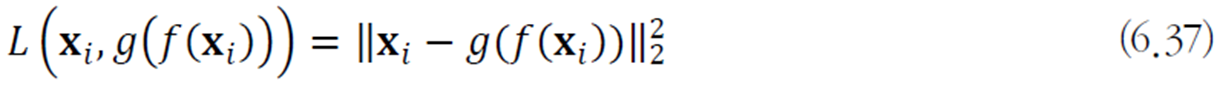
여기서 여러가지 규제 기법으로 적용하여 단순히 복사를 하는 경우를 피할 수 있다.
SAE(sparse autoencoder)
은닉 벡터
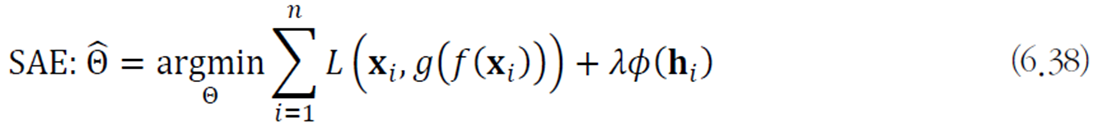
DAE(denoising autoencoder)
잡음을 추가한 다음 원본을 복원하도록 학습하는 원리이다.
특징벡터
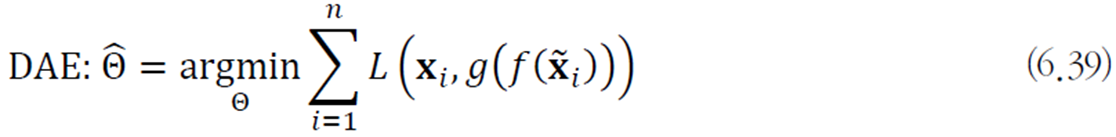
CAE(contractive autoencoder)
인코더 함수
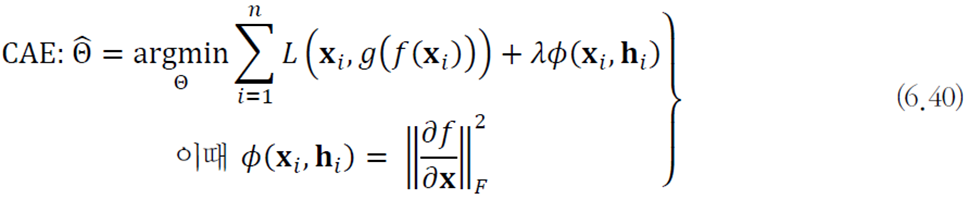
이는 공간을 축하는 효과를 지닌다.
적층 오토인코더
오토인코더는 은닉층이 하나인 얕은 신경망을 사용하기에 표현력에 한계가 있다. 따라서 여러 층으로 쌓아 용량을 키운다.
층별로 예비학습을 시켜 적층시킨다.
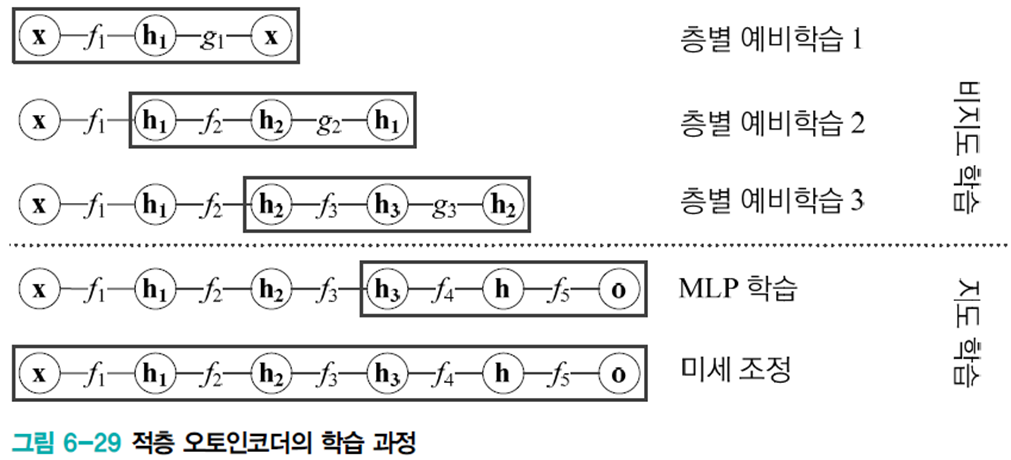
이 방식은 역사적 의미를 가지나 여러가지 기술 향상으로 현재는 층별 예비학습을 별로 사용하지 않는다.
매니폴드 학습
오토인코더는 데이터 구조를 간접적으로 표현한다. 반면 매니폴드 학습은 데이터의 비선형 구조를 상대적으로 직접적으로 반영한다. (점들간의 거리관계 등)
매니폴드

매니폴드는 고차원 공간에 내재한 저차원 공간이다.
오른쪽 그림에선 도로가 매니폴드에 해당한다.
보통 매니폴드는 비선형 공간이지만 지역적으로 살피면 선형 구조이다.
매니폴드 가정
고차원 공간에 주어진 실제 세계의 데이터는 고차원 입력 공간에 내재한 훨씬 저차원인 차원 매니폴드 인근에 집중되어 있다.
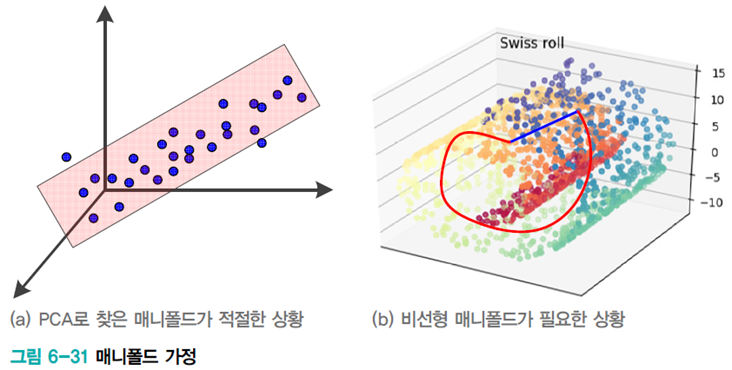
매니폴드를 찾는 방법, 표현하는 방법
IsoMap
최근접 이웃 그래프를 구축한다.
- 각 점은
- 빈 곳은 최단 경로의 길이로 채운다.
- 이들 고유 벡터가 새로운 저차원 공간을 령성한다.
단
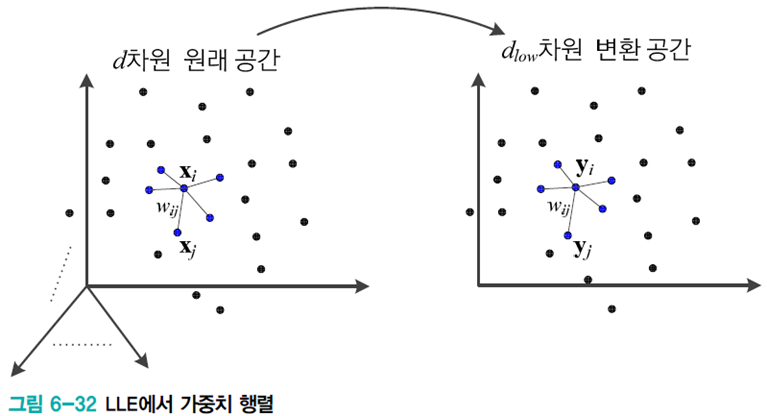
LLE(locally linear embedding)
거리 행렬
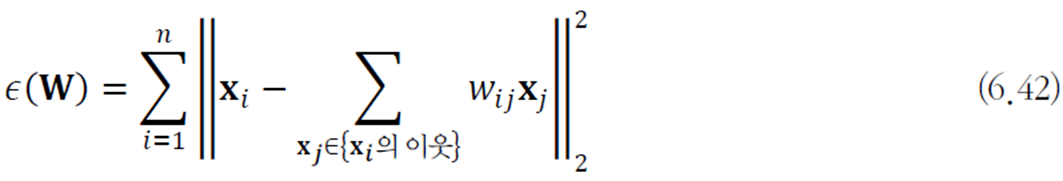
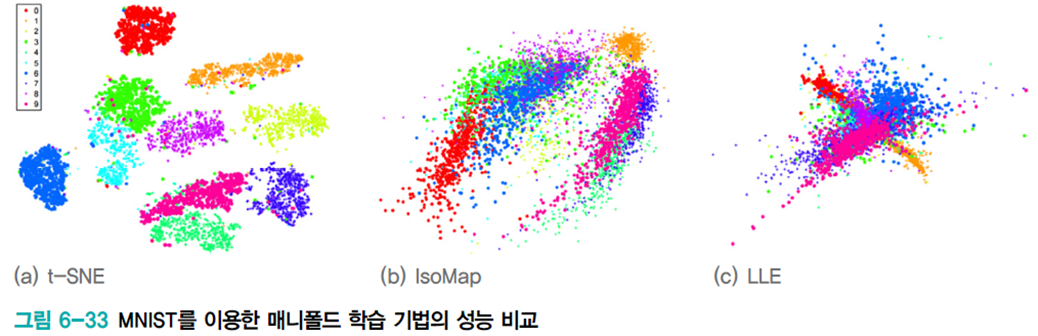
t-SNE(stochastic neighbor embedding)
현재 매니폴드 공간 변환 기법 중에서 가장 뛰어나다.
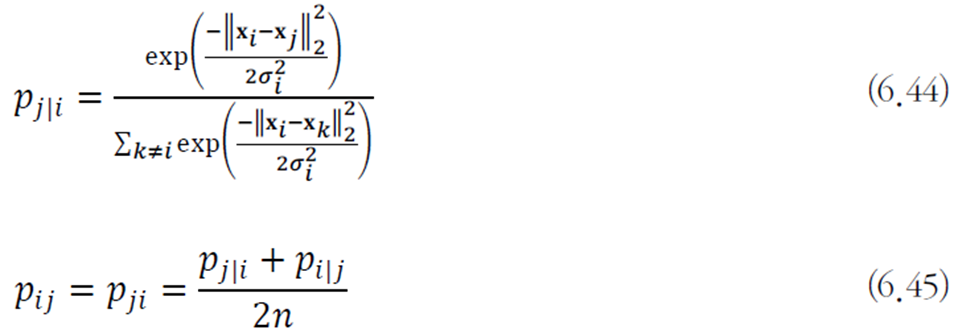
변환된 공간에서의 유사도는 스튜던트 t 분포로 측정한다.
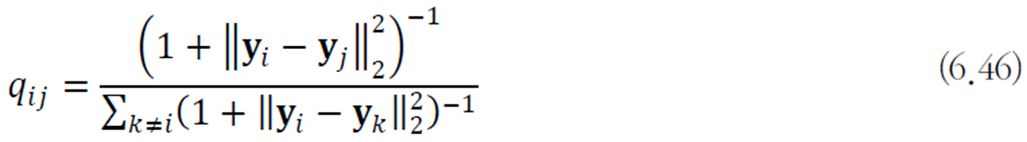
원래 데이터와 변환된 데이터의 구조가 비슷해야 하므로 확률분포
이 비슷한 정도는 KL 다이버전스로 측정한다.
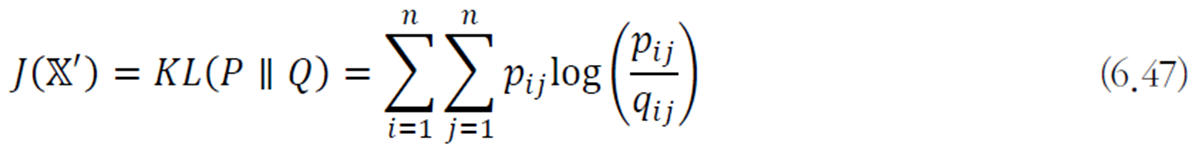
학습 알고리즘은 다음과 같이 정의된다.
목적함수
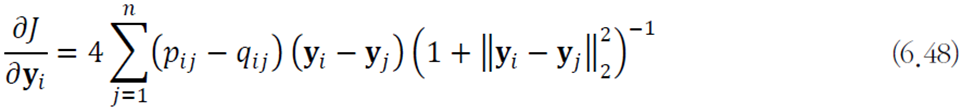

귀납적 학습 모델과 트랜스덕티브 학습 모델
트랜스덕티브 학습 모델
- 훈련집합 이외의 새로운 샘플을 처리할 능력이 없는 모델
- IsoMap, LLE, t-SNE는 모드 트랜스덕티브 모델이다.
- 데이터 가시화라는 목적에 관한 한 PCA나 오토인코더와 같은 귀납적 모델보다 성능이 뛰어나다.
어떤 문제를 풀 때 데이터가 제한되어 있으면 그 문제를 직접 풀어야 한다. 중간 문제로서 좀 더 일반적인 문제를 풀 필요가 없다.
귀납적 모델
- 훈련집합 이외의 새로운 샘플을 처리할 능력이 있는 모델
- IsoMap, LLE, t-SNE를 제외한 지금까지 공부한 모든 모델(CNN, DMLP 등)
주어진 문제에 따라 둘 중 더 적절한 것을 선택하는 지혜가 필요하다.
'공부한 내용 정리 > 인공지능' 카테고리의 다른 글
| [논문 리뷰]Few-shot learning for short text classification (0) | 2023.04.06 |
|---|---|
| 인공지능 기초 4 (1) | 2023.03.25 |
| 인공지능 기초 2 (0) | 2023.03.13 |
| [논문 리뷰]Latent Aspect Rating Analysis on Review Text Data:A Rating Regression Approach (0) | 2023.02.27 |
| 인공지능 기초 1 (0) | 2023.02.24 |
