티스토리 뷰
들어가며
본 게시물은 오일석 교수님의 기계학습 강의 8장을 보고 정리한 글입니다.
시간성 데이터(temporal data)
특징이 순서를 가지므로 순차 데이터(sequence)라 부른다. 이 순차 데이터는 보통 동적이며 가변적이다.
순환 신경망과 LSTM
순환 신경망은 시간성 정보를 활용하여 순차 데이터를 처리하는 효과적인 학습 모델이다. 문장이 긴 순차 데이터를 처리할 때는 장기 의존성을 더 잘 다루는 LSTM을 주로 활용한다.
순차 데이터
길이가 가변적이며 매 순간 값이 하나가 아닌 여러 개가 들어올 수 있다.
따라서 데이터를 표현할 때 벡터의 벡터로 표현한다. \(T\)번째 순간에 값이 여러 개 들어오므로 벡터가 요소가 된다.

훈련집합은 다음과 같이 표기한다.

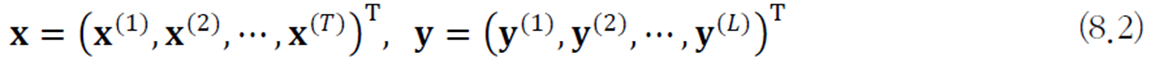
만약 \(\textbf{x}\)가 "April is the cruelest month." 이고 \(\textbf{y}\)가 "사월은 가장 잔인한 달" 일 때 사전을 이용하여 데이터를 위 식에 맞게 표현한다.
사전 구축 방법 : 사람이 사용하는 단어를 모아 구축, 또는 주어진 말뭉를 분석하여 단어를 자동 추출하여 구축한다.
사전을 사용한 텍스트 순차 데이터의 표현 방법은 다음과 같은 방법들이 있다.
- 단어가방(BoW : bag of words)
- 원 핫 코드
- 단어 임베딩
단어가방
단어 각각의 빈도수를 세어 \(m\)차원의 벡터로 표현한다. (\(m\)은 사전의 크기이다.)
만약 사전의 크기가 3만이라고 할 때 \(\textbf{x}\)는 "April", "is", "the", "cruelest", "month" 만 1이고 나머지는 0인 벡터가 된다.
이는 정보 검색에 주로 사용되나 이와 같이 데이터를 표현하면 시간성 정보가 사라진다는 한계가 있어 기계학습에선 부적절하다.
(“April is the cruelest month”와 “The cruelest month is April”은 같은 특징 벡터로 표현)
원핫 코드
해당 단어의 위치만 1로 표현한다.
ex) “April is the cruelest month”는 \(\textbf{x}=\left ( \left ( 0,0,1,0,0,0,\cdots \right )^{T} \left ( 0,0,1,0,0,0,\cdots \right )^{T}, \cdots \right )^{T}\)과 같이 표현된다. 이는 \(m\)차원 벡터를 요소로 가진 5차원 벡터이다.
이는 한 단어를 표현하는 데 \(m\)차원 벡터를 사용하는 비효율성을 지니며 단어 간의 유사도를 측정할 수 없다.
단어 임베딩
요즘 많이 쓰이는 기법이다. (강의 당시 2018년)
말뭉치에서 단어 간의 상호작용을 분석하여 새로운 공간으로 변환하는 기법이다. 보통 \(m\)보다 낮은 차원으로 변환한다.
변환 과정은 말뭉치를 훈련집합으로 사용하여 알아낸다.
개념이 가까운 것은 벡터도 가까이, 먼 것은 벡터도 멀리 위치한다.

순차 데이터의 특징
특징이 나타나는 순서가 중요하다.
ex) "내려갈 때 보았네"를 "때 내려갈 보았네"로 바꾸면 의미가 크게 훼손된다.
샘플의 길이가 다르다.
MLP, CNN의 경우 같은 크기의 데이터를 요구하기에 이런 경우 부적합하다. 그러나 순환 신경망의 경우 은닉층 순환 에지를 부여하여 가변 길이를 수용한다.
문맥 의존성
비순차 데이터의 경우 공분산이 특징 사이의 의존성을 나타낸다.
순차 데이터의 경우 공분산은 의미가 없고 문맥 의존성이 중요하다.
ex) "그녀는 점심때가 다 돼서야 ... 아점을 먹었는데 철수는 ..."에서 "그녀는"과 "먹었는데" 사이에 강한 문맥 의존성이 존재한다.
만약 둘 사이의 간격이 크면 장기 의존성이라 부른다.
순환 신경망 (RNN : Recurrent Neural Network)
RNN이 갖추어야 할 세 가지 필수 기능
- 시간성 : 특징을 순서대로 한 번에 하나씩 입력해야 한다.
- 가변 길이 : 길이가 \(T\)인 샘플을 처리하려면 은닉층이 \(T\)번 나타나야 한다. \(T\)는 가변적이다.
- 문맥 의존성 : 이전 특징 내용을 기억하고 있다가 적절한 순간에 활용해야 한다.
RNN 구조
MLP와 유사하게 입력층, 은닉층, 출력층을 갖는다.
특징점은 은닉층이 순환 에지(recurrent edge)를 갖는다. 순환 에지는 \(t-1\) 순간에 발생한 정보를 \(t\) 순간으로 전달하는 역할을 한다.
이렇게 함으로써 시간성, 가변 길이, 문맥 의존성을 모두 처리할 수 있다.
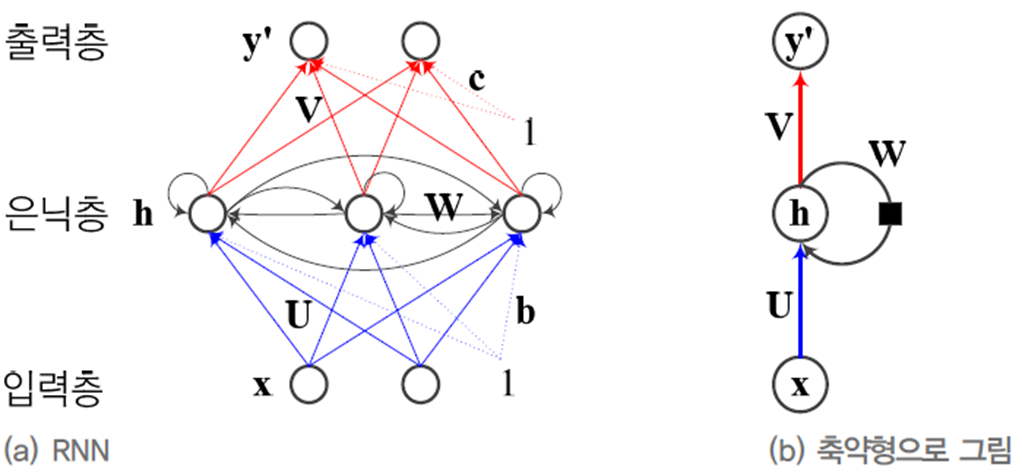
이를 수식으로 쓰면 다음과 같다.

\(t\) 순간에 은닉층 값 \(\textbf{h}^{(t-1)}\)과 \(t\) 순간의 입력 \(\textbf{x}^{(t)}\)를 받아 \(\textbf{h}^{(t)}\)로 변환한다.
이 RNN 식과 그림을 풀면 다음과 같다.


(이 부분은 강의 소리가 깨져 ppt만 보고 작성하였습니다.)
RNN의 매개변수는 \(\Theta = \left\{ \mathbf{U,W,V,b,c} \right\}\)
- \(\textbf{U}\)는 입력층과 은닉층을 연결하는 p*d 행렬
- \(\textbf{W}\)는 은닉층과 은닉층을 연결하는 p*p 행렬
- \(\textbf{V}\)는 은닉층과 출력층을 연결하는 q*p 행렬
- \(\textbf{b,c}\)는 바이어스로서 각각 p*1과 q*1 행렬
각 매개변수는 매 순간 다른 값을 사용하지 않고 같은 값을 공유한다. 공유를 함으로써 다음의 장점을 얻을 수 있다.
- 추정할 매개변수의 수가 획기적으로 줄어든다.
- 매개변수의 수가 특징 벡터의 길이 \(T\)에 무관해진다.
- 특징이 나타나는 순간이 뒤바뀌어도 같거나 유사한 출력을 만들 수 있다. ("어제 이 책을 샀다"와 "이 책을 어제 샀다"를 비슷한 영문장으로 번역 가능)
RNN은 출력 개수에 따라 여러가지 구조를 가진다. 예시로 아래 이미지에서 왼쪽은 출력을 하나만 가지는 경우, 오른쪽은 \(L\)개 가지는 경우이다.

RNN의 동작
\(\textbf{u}_{j}=\left ( \mathbf{u_{j1}, u_{j2}, \cdots ,u_{jd}} \right ) \)는 \(\textbf{U}\) 행렬의 \(j\) 번째 행을 의미하며 이들은 \(h_{j}\)에 연결된 에지의 가중치들이다.


RNN 계산
은닉층의 계산은 다음의 식으로 정의된다.

여기서의 계산은 \(\mathbf{a}_{j}\mathbf{h}^{(t-1)}\) 항을 제외하면 MLP와 유사하다.
행렬표기로 쓰면 다음과 같다.

출력층의 연산은 MLP와 똑같다.

RNN의 기억 기능
\(\textbf{x}^{(1)}\)이 변하면 상태 \(\textbf{h}^{(1)},\textbf{h}^{(2)},\textbf{h}^{(3)},\textbf{h}^{(4)}\)가 바뀌고, 그에 따라 출력 \(\textbf{y'}^{(1)},\textbf{y'}^{(2)},\textbf{y'}^{(3)},\textbf{y'}^{(4)}\)가 바뀐다. 이는 RNN이 \(\textbf{x}^{(1)}\)을 기억한다고 말할 수 있다.
또한 \(\textbf{x}^{(1)}\)은 \(\textbf{x}^{(2)},\textbf{x}^{(3)},\textbf{x}^{(4)}\)와 상호작용 하므로 문맥 의존성을 처리한다고 바라볼 수 있다.
BPTT(BackPropagation Through Time) 학습
RNN에서의 역전파 방법을 의미한다.
훈련집합 \(\mathbb{X}\)와 \(\mathbb{Y}\)에서 샘플 \(\mathbf{x}_{i}\)와 \(\mathbf{y}_{i}\)는 각각 길이가 \(T_{i}\)와 \(L_{i}\)인 시간성 데이터이다. (각 샘플은 요소가 벡터인 벡터)
BPTT를 이해하기 위해선 RNN과 DMLP의 유사성과 차별성을 이해해야 한다.
유사성
두 모델 모두 입력층, 은닉층, 출력층을 지닌다.

차별성
- DMLP는 샘플마다 은닉층의 수가 고정되어 있지만 RNN은 샘플에 따라 은닉층의 수가 달라진다.
- DMLP는 왼쪽에 입력, 오른쪽에 출력이 있지만 RNN은 매 순간마다 입력과 출력이 있다.
- DMLP는 은닉층마다 가중치가 다르지만 RNN은 가중치를 전체 은닉층이 공유한다.
BPTT의 목적함수
대체로 역전파와 비슷하지만 다른점이 존재한다.
비슷한 점은 목적함수로 평균제곱 오차, 교차 엔트로피, 로그우도 같은 것을 사용한다는 점이다.
그러나 다른 점은 매 순간마다 출력이 나오기 때문에 매 순간마다 손실을 계산하여 더한다.

BPTT 알고리즘이 해야 할 일을 형식화하면 다음과 같다.

그레이디언트 계산
\(\frac{\partial J}{\partial \Theta}\)을 계산하기 위해선 \(\Theta = \left\{ \mathbf{U,W,V,b,c} \right\}\) 이므로 \(\frac{\partial J}{\partial \mathbf{U}}, \frac{\partial J}{\partial \mathbf{W}}, \frac{\partial J}{\partial \mathbf{V}}, \frac{\partial J}{\partial \mathbf{b}}, \frac{\partial J}{\partial \mathbf{c}} \)를 계산해야 한다.
\(\frac{\partial J}{\partial \mathbf{V}}\)의 가중치를 예시로 들어보면 다음과 같다.
\(\frac{\partial J}{\partial \mathbf{V}}\)는 \(q*p\) 행렬이다.


목적함수를 로그 우도라 하고 연쇄법칙을 적용하여 \(J(\Theta )=-\textrm{log} y'^{(t)}\)를 \(t\) 순간에 \(v_{12}\)로 미분하면 다음과 같다.

맨 오른쪽 항 \(o_{1}^{(t)}\)는 다음과 같다.

따라서 \(\frac{\partial o_{1}^{(t)}}{\partial v_{12}}=h_{2}^{t}\)이다.
앞의 2개 항의 계산은 클래스가 2개일 때를 가정하면 \(\textbf{y}^{(t)}=(1,0)^{T}\)인 경우와 \(\textbf{y}^{(t)}=(0,1)^{T}\)인 경우로 나누어 생각해야 한다.
\(\textbf{y}^{(t)}=(1,0)^{T}\)인 경우의 계산은 다음과 같다.

\(\textbf{y}^{(t)}=(0,1)^{T}\)인 경우도 위와 같은 방식으로 유도하면 다음과 같은 결과가 나온다.

\(v_{12}\)를 \(v_{ji}\)로, 2부류를 \(q\)개 부류로 일반화하면 다음과 같다.

좀 더 간결히 표현하면 다음과 같다.

\(1,2,\cdots ,T\) 순간을 모두 고려하면 다음의 식으로 표현할 수 있다.

지금까지 \(\frac{\partial J}{\partial \mathbf{v_{ji}}}\)에 대한 과정이었다. 이를 행렬 전체를 위한 식 \(\frac{\partial J}{\partial \mathbf{\textbf{V}}}\)로 확장하고 \(\frac{\partial J}{\partial \mathbf{U}}, \frac{\partial J}{\partial \mathbf{W}}, \frac{\partial J}{\partial \mathbf{b}}, \frac{\partial J}{\partial \mathbf{c}} \)까지 유도하면 BPTT가 완성된다.
이 과정을 위해 식 (8.16)을 벡터 형태로 일반화하면 다음의 식이 나온다.

다음으로 은닉층에서의 미분을 유도할 것이다.
\(t\) 순간의 은닉층값 \(\textbf{h}^{(t)}\)는 그 이후의 은닉층과 출력층에 영향을 주므로 앞서 본 \(\textbf{V}\)로 미분하는 것보다 복잡하다.따라서 더 이상 이후가 없는 마지막 순간 \(T\)에 대하 미분식을 유도하고 그 전 순간을 유도하여 일반화된 식을 유도할 것이다.
우선 \(T\) 순간에 대한 미분식은 다음과 같다.
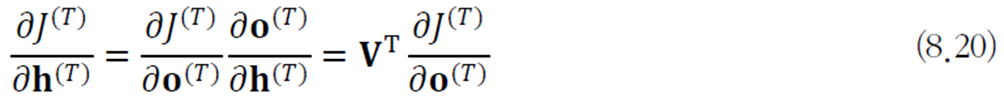
\(T-1\) 순간의 그레이디언트를 유도하면 다음과 같다.

여기서 \(\textbf{D}\left ( 1-\left ( \textbf{h}^{(T)} \right )^{2} \right )\)는 \(i\)번 열의 대각선이 \(1-\left ( \textbf{h}^{(T)} \right )^{2}\)을 가지는 대각 행렬이다.
이를 \(t\) 순간으로 일반화하면 다음의 그레이디언트를 연전파하는 순환식을 얻는다.

여기서 \(J^{(\widetilde{t})}\)는 \(t\)를 포함하여 이후에 목적함숫값을 모두 더한 \(J^{(\widetilde{t})}=J^{(t)}+J^{(t+1)}+\cdots +J^{(T)}\) 값이다.
다음 그림은 위 식을 그림으로 설명한 것이다.

다른 파라미터의 식까지 다 정리하면 다음과 같다.

(여기서부터도 강의 소리가 깨지고 대부분 영상 자체가 올라와 있지 않아 ppt를 보고 정리했습니다.)
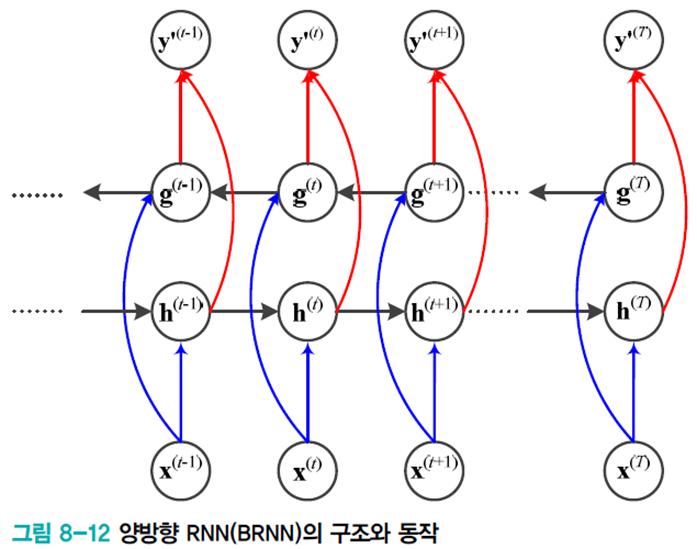
양방향 RNN
문맥 의존성은 기존 단방향 RNN처럼 왼쪽에서 오른쪽으로만 흐르지 않는다. 따라서 양방향 RNN(BRNN)은 \(t\) 순간에 앞쪽 입력과 뒤쪽 입력 정보를 모두 보고 처리한다.
장기 문맥 의존성
관련된 요소가 멀리 떨어져 영향력 감쇠가 일어나는 상황을 의미한다. 예를 들어 다음 문장에서 '길동은'과 '쉬기로'는 아주 밀접한 관련이 있다.


RNN 문제점
은닉층 사이의 가중치 \(\textbf{W}\)가 1보다 작을 때 일어나는 그레이디언트 소멸 또는 1보다 클 때 일어나는 그레이디언트 폭발이란 문제를 지닌다.
긴 입력 샘플의 입력이 자주 발생하고 가중치를 공유하며 같은 값을 계속 곱하기 때문에 DMLP나 CNN보다 이 문제가 더 심각하다.
이를 해결하기 위한 해결책으로 LSTM이 가장 널리 사용된다.
LSTM(Long Short Term Memory)
LSTM은 게이트를 이용하여 영향력 범위를 확장한다.
다음 그림처럼 게이트의 개폐를 통해 영향력을 조절한다. 실제로는 [0, 1] 사이의 실숫값으로 개폐 정도를 조절한다.

RNN과 LSTM 비교
다음 그림은 RNN과 LSTM의 구조를 비교한 것이다.

RNN의 은닉 노드를 확대하여 살펴보면 다음과 같다.

LSTM에선 가중치와 신호 값에 따라 입력 게이트와 출력 게이트의 개폐 정도를 조절한다. 만약 둘을 1.0으로 고정하면 RNN의 동작과 동일하다.

LSTM의 동작
LSTM의 가중치는 은닉층과 은닉층을 잇는 순환 에지에서 세 종류의 가중치를 갖는다.
- \(\textbf{W}^{g}\) : 입력단과 연결
- \(\textbf{W}^{i}\) : 입력 게이트와 연결
- \(\textbf{W}^{o}\) : 출력 게이트와 연결
이를 가중치 행렬로 표현하면 다음과 같다.

\(g, i, o\) 값은 가중치 \(\textbf{u, w}\)와 현재 순간의 입력벡터 \(\textbf{x}^{(t)}\), 이전 순간의 상태 \(\textbf{h}^{(t-1)}\)에 따라 정해진다.

\(\tau_{g}\)는 tanh, \(\tau_{f}\)는 로지스틱 시그모이드를 주로 사용한다.
아래쪽 곱 기호 *는 개폐를 조절한다. 입력 게이트의 값 \(i\)가 0.0에 가깝다면 \(g*i\)는 0.0에 가깝게 되어 입력단을 차단하게 되고 1.0에 가까우면 그대로 전달한다.
기호 /가 붙어 있는 원은 메모리 블록의 상태이다. 메모리 블록이 기억하는 내용을 의미하며 시간에 따라 변하므로 \(s^{(t)}\)로 표기한다.
\[s^{(t)}=s^{(t-1)}+g*i\]
이 식의 의미는 입력 게이트가 0.0이면 \(g*i\)도 0이 되어 이전 상태와 같게 된다는 의미다. 이는 이전 입력의 영향력을 더 멀리 확장하는 효과를 갖게 된다.
위쪽 곱 기호 *도 마찬가지로 출력 게이트의 값 \(o\)의 개폐 정도를 조절한다.
\[h_{j}^{(t)}=\tau_{h}(s^{(t)})*o\]
이렇게 구해진 \(h_{j}^{(t)}\)는 \(q\) 개의 출력 노드로 전달되어 출력단 계산에 사용된다. 또한 다음 순간에 연산에 사용된다.
지금까지의 수식을 정리하면 다음과 같다.

추가로 망각 게이트라는 것이 존재한다. 이는 이전 순간의 상태 \(h^{(t-1)}\)를 지우는 효과를 지닌다.

망각 게이트를 추가한 식은 다음과 같다.
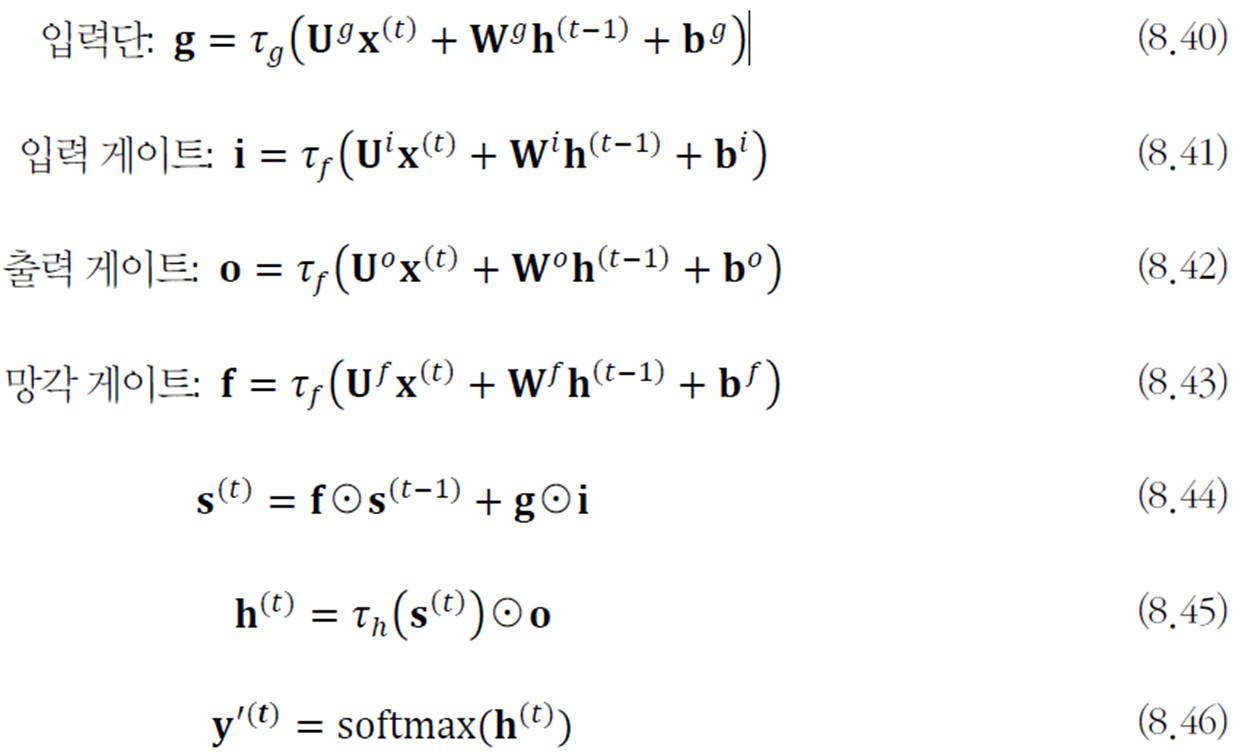
추가로 LSTM에 핍홀 기능을 추가한다. 핍홀은 블록의 내부 상태를 입력 게이트, 출력 게이트, 망각 게이트 각 3개의 게이트에 알려주는 역할을 한다. (각 게이트에 인자로 메모리 블록으로 넘겨준다는 것으로 이해했음)
이는 음성 인식을 수행하다가 특정 단어가 발견되면 지정된 행위를 수행하는 등의 순차 데이터를 처리하다가 어떤 조건에 따라 특별한 조치를 취해야 하는 응용에 효과적이다.

응용 분야
언어 모델
언어 모델이란 단어 열의 확률분포를 의미한다. ex) \(P(자세히, 보아야, 예쁘다) > P(예쁘다, 보아야, 자세히)\)
이를 활용하여 음성 인식기 혹은 언어 번역기가 후보로 출력한 문장이 여럿 있을 때 확률을 계산하여 확률이 가장 높은 것을 선택한다.
확률 분포를 추정하는 방법으론 \(n\)-그램, 다층 퍼셉트론, 순환 신경망이 대표적이다.
\(n\)-그램
기계 학습 이전에 사용하던 고전적인 방법이다.
문장을 \(\textbf{x}=\left (\mathrm{z_{1},z_{2},\cdots ,z_{T}} \right )^{T}\)라 하면 \(\textbf{x}\)가 발생할 확률을 다음 식으로 추정한다.

\(n\)-그램은 \(n-1\) 개의 단어만 고려하므로 다음 식이 성립한다.

알아야 할 확률의 개수는 \(m^{n}\) 개이므로 차원의 저주 때문에 \(n\)을 1~3 정도로 작게 해야만 한다. 또한 단어가 원핫 코드로 표현되므로 단어 간의 의미있는 거리를 반영하지 못하는 한계가 있다.
순환 신경망
이 방법은 순환 신경망을 이용해 현재까지 본 단어 열을 기반으로 다음 단어를 예측하는 방식으로 학습하여 확률 분포 추정 뿐만 아니라 문장 생성 기능까지 갖춘다.
이는 비지도 학습에 해당하여 말뭉치로부터 쉽게 훈련집합 구축이 가능하다.
예시로 "자세히 보아야 예쁘다"라는 문장은 다음과 같은 샘플이 된다.

일반화하면 다음과 같이 표현할 수 있다.


순환 신경망은 훈련집합으로 말뭉치에 있는 식을 (8.49)처럼 변환하여 BPTT를 통해 학습을 한다.
이렇게 훈련을 마친 언어모델은 기계 번역기나 음성 인식기의 성능을 향상시키는 데 활용한다.
또한 생성 모델로 활용될 수 있다.

기계 번역

언어 모델보다 어려운 과업이다. 언어 모델의 경우 입력 문장과 출력 문장의 길이가 같지만 기계 번역은 길이가 서로 다른 열 대 열(sequence to sequence) 문제이며 어순도 다르다.
예전의 통계적 기계 번역 방법의 한계로 현재는 딥러닝에 기반한 신경망 기계 번역 방법이 주류이다.
기계 번역 방법 중 하나는 LSTM을 사용하여 번역 과정 전체를 통째로 학습하는 방법이다.
인코더와 디코더로 LSTM 2개를 사용한다.
인코더는 원시 언어 문장을 특징 벡터로 변환하고 디코더는 특징 벡터로 목적 언어 문장을 생성한다.

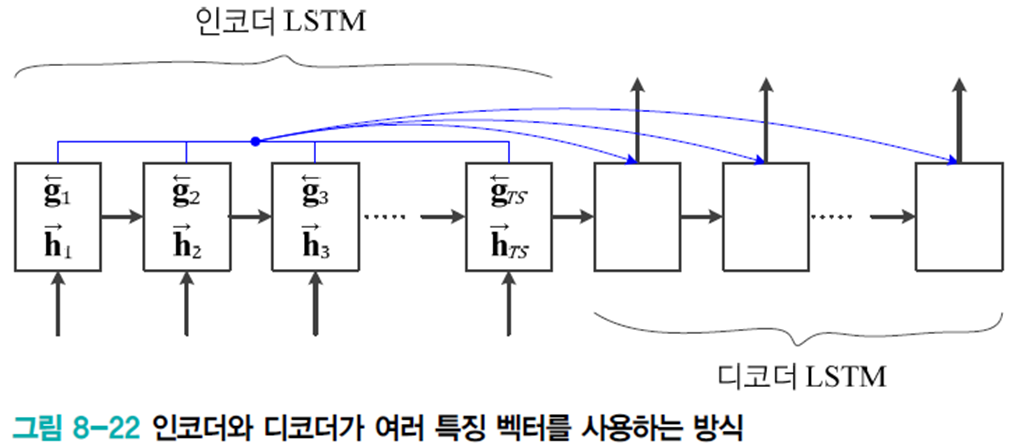
또 다른 방법은 모든 순간의 상태 변수를 사용하는 방법이다. (attention을 의미하는 것 같음)
인코더의 계산 결과를 모두 디코더에 넘겨주고 양방향 구조를 채택하여 어순이 다른 문제를 해결한다.
영상 주석 생성

영상 속 물체를 검출하고 인식, 물체의 속성과 행위, 물체 간의 상호 작용을 알아내는 일, 의미를 요약하여 문장을 생성하는 일을 복합적으로 매우 도전적인 문제이다.
예전에는 물체 분할, 인식, 단어 생성과 조립 단계를 따로 구현한 후 연결하는 접근 방법을 채택했지만 현재는 딥러닝 기술을 사용하여 통째 학습(end-to-end)을 한다.
딥러닝 접근 방법은 CNN으로 영상을 분석하고 인식하여 LSTM을 통해 문장을 생성한다.

훈련집합으론 \(\textbf{x}\)는 영상, \(\textbf{y}\)는 영상을 기술하는 문장으로 표현된다.

CNN은 입력 영상을 단어 임베딩 공간의 특징벡터로 변환한다.

훈련 샘플 \(\textbf{y}\)의 단어 \(\textbf{z}_{t}\)는 단어 임베딩 공간의 특징 벡터 \(\widetilde{z}_{t}\)로 변환된다. 이는 행렬 \(\textbf{E}\)를 이용하여 변환되며 통째 학습 과정에서 CNN, LSTM과 동시에 최적화 된다.
'공부한 내용 정리 > 인공지능' 카테고리의 다른 글
| [RecSys] Modern Recommendation Systems with Neural Networks (0) | 2023.04.12 |
|---|---|
| [논문 리뷰]Few-shot learning for short text classification (0) | 2023.04.06 |
| 인공지능 기초 3 (0) | 2023.03.20 |
| 인공지능 기초 2 (0) | 2023.03.13 |
| [논문 리뷰]Latent Aspect Rating Analysis on Review Text Data:A Rating Regression Approach (0) | 2023.02.27 |
